

分析 (1)与圆内接四边形的性质得出∠A+∠C=180°,由三角形内角和定理得出∠C+∠BDC+∠DBC=180°,得出∠A=∠BDC+∠DBC,再由已知条件证出BDC=∠DBC,即可得出结论;
(2)连接OC交BD于M,延长DO交⊙O于N,由(1)得:CB=CD,得出$\widehat{CB}=\widehat{CD}$,由才知道了得出OC⊥BD,BM=DM=$\frac{1}{2}$BD,∠BMC=90°,证出四边形BECM是矩形,得出BM=CE,由角平分线得出∠ADN=∠BDN,由圆周角定理证出$\widehat{AN}=\widehat{BN}$,由垂径定理得出DN垂直平分AB,证出AD=BD,即可得出结论;
(3)在AC上截取AF=BC=5,连接DF,过D作DG⊥AC于G,过B作BH⊥AC于H,连接OC,如图2所示:由(2)得:AD=BD=2CE,由ASA证明△DAF≌△DBC,得出DF=DC=5,由等腰三角形的性质得出CG=FG=3,求出AG=AF+FG=8,由勾股定理求出DG=4,由三角函数求出tan∠DAG=$\frac{DG}{AG}$=$\frac{1}{2}$,证出∠BAC=∠DAG,得出∠BAC=$\frac{BH}{AH}$=$\frac{1}{2}$,得出AH=2BH,设BH=x,AH=2x,则CH=11-2x,在Rt△BCH中,由勾股定理得出方程,解方程求出BH,求出△ABC的面积,证出CE为⊙O的切线,由弦切角定理得出∠BCE=∠BCA,由三角函数得出BE=$\sqrt{5}$,CE=2$\sqrt{5}$,求出△BCE的面积,得出四边形ACEB的面积=△ABC的面积+△BCE的面积$\frac{157}{5}$.
解答  (1)证明:如图1所示:
(1)证明:如图1所示:
∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∵∠C+∠BDC+∠DBC=180°,
∴∠A=∠BDC+∠DBC,
∵∠BAD=2∠BDC,
∴∠BDC=∠DBC,
∴BC=CD;
(2)证明:连接OC交BD于M,延长DO交⊙O于N,如图2所示:
由(1)得:CB=CD,
$\widehat{CB}=\widehat{CD}$,
∴OC⊥BD,
∴BM=DM=$\frac{1}{2}$BD,∠BMC=90°,
∵CE∥DB,
∴∠MCE=180°-90°=90°,
又∵BE⊥CE,
∴∠BEC=90°,
∴四边形BECM是矩形,
∴BM=CE,
∵OD平分∠ADB,
∴∠ADN=∠BDN,
∴$\widehat{AN}=\widehat{BN}$,
∴DN垂直平分AB,
∴AD=BD,
∴AD=2BM=2CE;
(3)解:在AC上截取AF=BC=5,连接DF,过D作DG⊥AC于G,过B作BH⊥AC于H,如图3所示: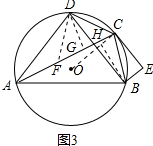
由(2)得:AD=BD=2CE,
∵AF=DF,
∴∠DAF=∠ADF,
∵∠DAF=∠DBC,∠BDC=∠DBC,
∴∠DAF=∠ADF=∠BDC=∠DBC,
在△DAF和△DBC中,$\left\{\begin{array}{l}{∠ADF=∠BDC}&{\;}\\{AD=BD}&{\;}\\{∠DAF=∠DBC}&{\;}\end{array}\right.$,
∴△DAF≌△DBC(ASA),
∴DF=DC=5,
∴CG=FG,
∵AC=11,
∴CG=FG=3,
∴AG=AF+FG=8,DG=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴tan∠DAG=$\frac{DG}{AG}$=$\frac{4}{8}$=$\frac{1}{2}$,
∵BC=CD,
∴$\widehat{BC}=\widehat{CD}$,
∴∠BAC=∠DAG,
∴tan∠BAC=$\frac{BH}{AH}$=$\frac{1}{2}$,
∴AH=2BH,
设BH=x,AH=2x,
∴CH=11-2x,
在Rt△BCH中,BH2+CH2=BC2,
即x2+(11-x)2=52,
解得:x=4(舍去),或x=$\frac{24}{5}$,
∴BH=$\frac{24}{5}$,
∴△ABC的面积=$\frac{1}{2}$AC•BH=$\frac{1}{2}$×11×$\frac{24}{5}$=$\frac{132}{5}$,
∵OC⊥BD,CE∥BD,
∴OC⊥CE,
∴CE为⊙O的切线,
∴∠BCE=∠BCA,
∴tan∠BCE=$\frac{BE}{CE}$=$\frac{1}{2}$,
∵BC=5,
∴BE=$\sqrt{5}$,CE=2$\sqrt{5}$,
∴△BCE的面积=$\frac{1}{2}$BE•CE=$\frac{1}{2}$×$\sqrt{5}$×2$\sqrt{5}$=5,
∴四边形ACEB的面积=△ABC的面积+△BCE的面积=$\frac{132}{5}$+5=$\frac{157}{5}$.
点评 本题是圆的综合题目,考查了圆内接四边形的性质,等腰三角形的判定,圆心角、弧、弦之间的关系、垂径定理、全等三角形的判定与性质、勾股定理、圆周角定理、切线的判定、弦切角定理、三角函数等知识;本题综合性强,难度较大,需要通过作辅助线才能得出结论.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 已知a、b、c是三角形的三边长,则a2+b2=c2 | |
| B. | 在直角三角形中,两边的平方和等于第三边的平方 | |
| C. | 在Rt△ABC中,∠C=90°,a、b、c分别是∠A,∠B,∠C的对边,则a2+b2=c2 | |
| D. | 在Rt△ABC中,∠B=90°,a、b、c分别是∠A,∠B,∠C的对边,则a2+b2=c2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}+\overrightarrow{BA}=0$ | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{CB}$ | D. | $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow 0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com