解:(1)∵关于x的方程x
2+(2k+m)x+(k
2+km)=0有两个相等的实数根,
∴△=(2k+m)
2-4(k
2+km)=m
2=0.
∴m=0.
(2)当m=0时,抛物线的解析式为y=2x
2-4x+2k+2.
它的对称轴为直线x=1,顶点D的坐标为D(1,2k).
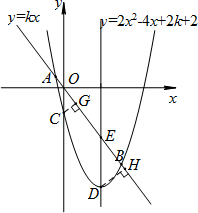
(3)∵k<-1,
∴2k+2<0,点C(0,2k+2)在y轴的负半轴上.
设抛物线的对称轴与直线AB的交点为E点,
则E点的坐标为E(1,k).
作CG⊥AB于G点,DH⊥AB于H点.(如图)
∵S
△ABD=2S
△ABC,
∴DH=2CG.
∵抛物线的对称轴与y轴平行,
∴∠COG=∠DEH.
∴sin∠COG=sin∠DEH.
可得 DE=2CO.
∴-k=-2(2k+2).
解得 k=-

.
分析:(1)一元二次方程有两个相等实数根时,根的判别式等于0,据此求解.
(2)将(1)得到的m值代入抛物线的解析式中,进行配方后能得到顶点D的坐标.
(3)首先画出对应的图形,若S
△ABD=2S
△ABC,那么对于两个同底不等高的三角形来说,它们的高的比等于1:2,过C、D作直线AB的垂线,通过构建相似三角形求出DE的长,由此求得k的值.
点评:该题主要考查了二次函数解析式的确定、根与系数的关系、图形面积的求法等知识;难点在于(3)题,将三角形的面积比转化高的比是打开思路的关键.

 已知:k,m为实数,且k<-1,关于x的方程x2+(2k+m)x+(k2+km)=0有两个相等的实数根.抛物线y=2x2-(6m+4)x+2k+2与直线y=kx的交点分别为A点,B点,与y轴的交点为C,顶点为D.
已知:k,m为实数,且k<-1,关于x的方程x2+(2k+m)x+(k2+km)=0有两个相等的实数根.抛物线y=2x2-(6m+4)x+2k+2与直线y=kx的交点分别为A点,B点,与y轴的交点为C,顶点为D. (3)∵k<-1,
(3)∵k<-1, .
.

