
����Ŀ���ס������ҳ���ͬ������ͬһ��ɲ��ʽ��������1����������1����������1ƿ��������Һ��ɣ���������Һ��Ϊ��Ʒ�ɵ�������1ƿ��������Һ���ۼ���1����������![]() ����֪��������Һ��������Ϊ20%��������������������Ϊ25%���Ű��̴Ӽ׳�������1��������������������������4ƿ��������Һ�����д��й�����10Ԫ��
����֪��������Һ��������Ϊ20%��������������������Ϊ25%���Ű��̴Ӽ׳�������1��������������������������4ƿ��������Һ�����д��й�����10Ԫ��
��1����1����������1ƿ��������Һ���ۼۣ�
��2��Ϊ�˴ٽ��ÿ������������ۣ��׳��д�8.5�����ۣ����ҳ��в��õ����۷����ǹ˿�ÿ��1����������1ƿ��������Һ������δ����ڼ䣬�׳�������2000�������������ҳ����������������ϻ�õ������ڼ׳��е�1.2�������ҳ����������۶�������������
���𰸡�(1)���������ۼ�30Ԫ����������Һ���ۼ�6Ԫ��(2)��3600
��������
���������(1)����1���������ۼ�5xԪ��1ƿ��������Һ���ۼ�xԪ�����������г����̽�ɣ�
(2)�����ҳ�������x���������������ҳ����������������ϻ�õ������ڼ׳��е�1.2���г����̽�ɣ�
���������(1)����1���������ۼ�5xԪ��1ƿ��������Һ���ۼ�xԪ��
![]() �� ���x=6��
�� ���x=6��
������1���������ۼ�30Ԫ��1ƿ��������Һ���ۼ�6Ԫ��
(2)�����ҳ�������x���������� W��=2000����30��0.85��24��=3000Ԫ��
W��=x����30��24����x��5=x ������֪W����W�� ���x��3600��
�ҳ�����������3600����������


 ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д� ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�ADΪ����ֱ�ǡ�ABC�ĸߣ���A�͵�C�ֱ���������DEFG�ı�DG��DE�ϣ�����BG��AE��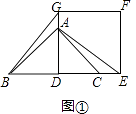
��1����֤��BG=AE��
��2����������DEFG�Ƶ�D��ת�����߶�EG������Aʱ������ͼ����ʾ��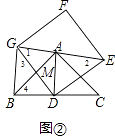
����֤��BG��GE��
����DG��AB���ڵ�M����AG��AE=3��4���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ1��AC��BD�ǶԽ��ߡ�����DCB���ŵ�D˳ʱ����ת45��õ���DGH��HG��AB�ڵ�E������DE��AC�ڵ�F������FG�������н��ۣ�
���ı���AEGF������ �ڡ�AED����GED
�ۡ�DFG=112.5�� ��BC+FG=1.5
������ȷ�Ľ����ǣ� ��
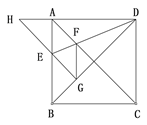
A. �٢ڢۢ� B. �٢ڢ� C. �٢� D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��E��AC��һ�㣬����A��AG��EB������ΪG��AG��BD��F����OE=OF��
��1����֤��0E=OF
��2�����1�����ijͬѧ���������²²⣺���������⣬����E��AC���ӳ����ϣ�AG��EB��AG�� EB���ӳ����� G��AG���ӳ��߽�DB���ӳ����ڵ�F�������������䣬������OE=OF���ʣ��²����ý����Ƿ�������������������֤����������������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���BAC=90�㣬O��AB���ϵ�һ�㣬��OAΪ�뾶�ġ�O���BC�����ڵ�E�� 
��1����AC=6��BC=10�����O�İ뾶��
��2������E����EF��AB��M������AF������AFE=2��ABC����֤���ı���ACEF�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC��AD����ABC�Ľ�ƽ���ߣ�DE��AB��DF��AC������ֱ�ΪE��F���������ĸ����ۣ���AD������һ�㵽��C��B�ľ�����ȣ���AD������һ�㵽AB��AC�ľ�����ȣ���BD��CD��AD��BC���ܡ�BDE����CDF.������ȷ�ĸ�����(����)

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��0��2������AOBΪ�ȱ������Σ�P��x����һ�����㣨����ԭO�غϣ������߶�APΪһ�������Ҳ����ȱ���������APQ��

��1�����B�����ꣻ
��2���ڵ�P���˶������У���ABQ�Ĵ�С�Ƿ����ı䣿�粻�ı䣬������С����ı䣬��˵�����ɣ�
��3������OQ����OQ��ABʱ����P������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ���A1C1C2���ܳ�Ϊ1����C1D1��A1C2��D1����C1C2���ӳ�����ȡ��C3��ʹD1C3=D1C1������D1C3����C2C3Ϊ�����ȱ���A2C2C3����C2D2��A2C3��D2����C2C3���ӳ�����ȡ��C4��ʹD2C4=D2C2������D2C4����C3C4Ϊ�����ȱ���A3C3C4�����ҵ�A1��A2��A3��������ֱ��C1C2ͬ�࣬�����ȥ������A1C1C2����A2C2C3����A3C3C4��������AnCnCn+1���ܳ���Ϊ______����n��2����nΪ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��ֱ��y=kx+4�����㣨1��2������ʽkx+4��0�Ľ⼯��
��2��xȡ��Щ������ʱ������ʽ x+3>6 �� 2x-1<10 ��������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com