Question

（1）如图，已知∠BAC+∠ACD=180°，AE平分∠BAC，CF平分∠ACG.则∠1与∠2的关系怎样？试证明你的结论．(要求写出推理过程和每一步的理由)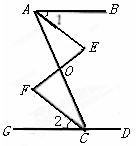

（2）若将（1）中的条件改为∠BAC=∠ACG，其它条件不变，则∠1与∠2的上述关系还成立吗？（直接写出结论即可）

Answer 1

（1）∠1＝∠2 ；（2）仍然成立

解析试题分析：（1）由∠BAC+∠ACD=180°可证得∥，即得∠BAC＝∠ACG，再根据角平分线的性质可得∠1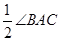＝，∠2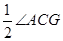＝，从而证得结论；
（2）证法同（1）.
（1）∠1＝∠2
∵∠BAC+∠ACD=180°，
∴∥（同旁内角互补，两直线平行）
∴∠BAC＝∠ACG（两直线平行，内错角相等）
又∵AE平分∠BAC，CF平分∠ACG ，
∴∠1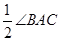＝，∠2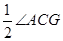＝ （角平分线的定义）
∴∠1＝∠2(等量代换) ；
（2）∠1＝∠2的结论仍然成立.
考点：平行线的判定和性质，角平分线的性质
点评：平行线的判定和性质是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.