
���� �ֱ���á�A1OB1����A2OB2���Լ���AnBnCn��������ܽ���ɣ�������ã�
��� �⣺y=-2x+1�зֱ���x=0��y=0����ã�y=1��x=$\frac{1}{2}$����ֱ����x���y�ύ��A1��B1���ֱ��ǣ�$\frac{1}{2}$��0����0��1�������A1OB1������O��ƽ��ֱ������ϵ��ԭ�㣩�����Ϊ$\frac{1}{2}$��1��$\frac{1}{2}$��
ͬ����A2OB2�����Ϊ��$\frac{1}{2}$��$\frac{1}{2}$��$\frac{1}{3}$��
��AnOBn�������$\frac{1}{2}$��$\frac{1}{n}$��$\frac{1}{n+1}$��
��S1+S2+��+S2016��ֵ$\frac{1}{2}��1��\frac{1}{2}+\frac{1}{2}��\frac{1}{2}��\frac{1}{3}+��+\frac{1}{2}��\frac{1}{2016}��\frac{1}{2017}$=$\frac{1}{2}����1-\frac{1}{2017}��=\frac{2016}{4034}$��
�ʴ�Ϊ��$\frac{2016}{4034}$��
���� ���⿼�鷴����������һ�κ����Ľ������⣬�ؼ�����ȷ������������ε������


 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д� Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
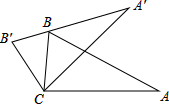 ��ͼ������ABC�ƶ���C��ת�õ���A��B��C���ҵ�B�պ�����A��B���ϣ�����A=25�㣬��BCA��=45�㣬���ABC���ڣ�������
��ͼ������ABC�ƶ���C��ת�õ���A��B��C���ҵ�B�պ�����A��B���ϣ�����A=25�㣬��BCA��=45�㣬���ABC���ڣ�������| A�� | 40�� | B�� | 55�� | C�� | 65�� | D�� | 70�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��������ֽƬABCD�ġ�C����GF�۵�����F��BC�ϣ�����B��C�غϣ���ʹ��C���ڳ������ڲ���E������FHƽ�֡�EFB�����GFH���ڣ�������
��������ֽƬABCD�ġ�C����GF�۵�����F��BC�ϣ�����B��C�غϣ���ʹ��C���ڳ������ڲ���E������FHƽ�֡�EFB�����GFH���ڣ�������| A�� | 80�� | B�� | 85�� | C�� | 90�� | D�� | 95�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y1��y2 | B�� | y1��y2 | C�� | y1=y2 | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com