
 ¾¹żµć
¾¹żµć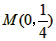 £¬Ņ»×éÅ×ĪļĻߵĶ„µćB1£Ø1£¬y1£©£¬B2£Ø2£¬y2£©£¬B3£Ø3£¬y3£©£¬”£¬Bn£Øn£¬yn£©£ØnĪŖÕżÕūŹż£©ŅĄ“ĪŹĒÖ±ĻßlÉĻµÄµć£¬Õā×éÅ×ĪļĻßÓėxÖįÕż°ėÖįµÄ½»µćŅĄ“ĪŹĒ£ŗA1£Øx1£¬0£©£¬A2£Øx2£¬0£©£¬A3£Øx3£¬0£©£¬”£¬An+1£Øxn+1£¬0£©£ØnĪŖÕżÕūŹż£©£¬Éčx1=d£Ø0£¼d£¼1£©”£
£¬Ņ»×éÅ×ĪļĻߵĶ„µćB1£Ø1£¬y1£©£¬B2£Ø2£¬y2£©£¬B3£Ø3£¬y3£©£¬”£¬Bn£Øn£¬yn£©£ØnĪŖÕżÕūŹż£©ŅĄ“ĪŹĒÖ±ĻßlÉĻµÄµć£¬Õā×éÅ×ĪļĻßÓėxÖįÕż°ėÖįµÄ½»µćŅĄ“ĪŹĒ£ŗA1£Øx1£¬0£©£¬A2£Øx2£¬0£©£¬A3£Øx3£¬0£©£¬”£¬An+1£Øxn+1£¬0£©£ØnĪŖÕżÕūŹż£©£¬Éčx1=d£Ø0£¼d£¼1£©”£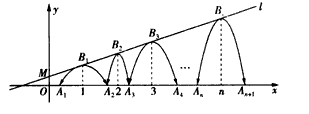
 ±øÕ½ÖŠæ¼ŗ®¼ŁĻµĮŠ“š°ø
±øÕ½ÖŠæ¼ŗ®¼ŁĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| ||
| 3 |
| 3 |
 ŌµćO¼°A”¢BĮ½µć£®
ŌµćO¼°A”¢BĮ½µć£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ½»ÓŚµćG£¬“¹×ć·Ö±šŹĒE”¢F£¬ACŹĒ”ŃOµÄĻŅ£¬
½»ÓŚµćG£¬“¹×ć·Ö±šŹĒE”¢F£¬ACŹĒ”ŃOµÄĻŅ£¬²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ŅŃÖŖ£ŗČēĶ¼£¬Ö±Ļßy=kx+b¾¹żµćA”¢B£®
ŅŃÖŖ£ŗČēĶ¼£¬Ö±Ļßy=kx+b¾¹żµćA”¢B£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ŅŃÖŖ£ŗČēĶ¼£¬Ö±Ļßy=kx+bÓėxÖį½»ÓŚµćA£¬ĒŅÓėĖ«ĒśĻßy=
ŅŃÖŖ£ŗČēĶ¼£¬Ö±Ļßy=kx+bÓėxÖį½»ÓŚµćA£¬ĒŅÓėĖ«ĒśĻßy=| m |
| x |
| m |
| x |
| m |
| x |
| m |
| x |
| 7 |
| 2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ŅŃÖŖ£ŗČēĶ¼£¬Ö±Ļßa”Īb£¬”Ļ1=£Ø2x+10£©”ć£¬”Ļ2=£Ø3x-5£©”ć£¬ÄĒĆ“”Ļ1=
ŅŃÖŖ£ŗČēĶ¼£¬Ö±Ļßa”Īb£¬”Ļ1=£Ø2x+10£©”ć£¬”Ļ2=£Ø3x-5£©”ć£¬ÄĒĆ“”Ļ1=²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com