
分析 (1)设$\sqrt{4-3x}$=t,(t≥0),则原函数化为y=-$\frac{2}{3}$(t-$\frac{3}{4}$)2+$\frac{73}{24}$,即可得出结论;
(2)设$\sqrt{1-{x}^{2}}$=t,(0≤t≤1),原代数式转化为y=(t-$\frac{1}{2}$)2+$\frac{11}{4}$,利用自变量的范围即可得出结论.
解答 解:(1)设$\sqrt{4-3x}$=t,(t≥0),
∴4-3x=t2,
∴x=$\frac{1}{3}$(-t2+4),
∴y=2×$\frac{1}{3}$(-t2+4)+t=-$\frac{2}{3}$(t2-$\frac{3}{2}$t)+$\frac{8}{3}$=-$\frac{2}{3}$(t-$\frac{3}{4}$)2+$\frac{73}{24}$,
∴当t=$\frac{3}{4}$,即:x=$\frac{55}{48}$时,y最大=$\frac{73}{24}$;
∴函数y=2x+$\sqrt{4-3x}$的最大值为$\frac{73}{24}$;
(2)∵1-x2≥0,
∴-1≤t≤1,
设$\sqrt{1-{x}^{2}}$=t,(0≤t≤1),
∴x2=1-t2,
设y=4-x2-$\sqrt{1-{x}^{2}}$=4-(1-t2)-t=t2-t+3=(t-$\frac{1}{2}$)2+$\frac{11}{4}$,
∵0≤t≤1,
∴当y有最小值时,t=$\frac{1}{2}$,即:$\sqrt{1-{x}^{2}}$=$\frac{1}{2}$,
∴x=±$\frac{\sqrt{3}}{2}$,
即:代数式4-x2-$\sqrt{1-{x}^{2}}$达到最小值时,x=±$\frac{\sqrt{3}}{2}$,
当y有最大值时,(t-$\frac{1}{2}$)2最大,
∴t=0或t=1,
当t=0时,x=±1,
当t=1时,x=0,
即:代数式4-x2-$\sqrt{1-{x}^{2}}$达到最大值时,x=±1或0,
故答案为±$\frac{\sqrt{3}}{2}$;±1或0.
点评 本题考查了函数的最值问题.解题时,采用了“换元法”和“转化思想”,将原问题转化为求函数的极值的问题,根据函数图象的增减性来求函数的极值.使问题变得形象、直观、简单了.


科目:初中数学 来源: 题型:填空题
 中国传统数学最重要的著作《九章算术》中记载:“今有牛五、羊二,直金十两:牛二、羊五,直金八两.问牛、羊各直金几何?”其译文是:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两,问每头牛、每只羊各值金多少两?”现设每头牛值金x两,每只羊值金y两,则可列方程组为$\left\{\begin{array}{l}{5x+2y=10}\\{2x+5y=8}\end{array}\right.$.
中国传统数学最重要的著作《九章算术》中记载:“今有牛五、羊二,直金十两:牛二、羊五,直金八两.问牛、羊各直金几何?”其译文是:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两,问每头牛、每只羊各值金多少两?”现设每头牛值金x两,每只羊值金y两,则可列方程组为$\left\{\begin{array}{l}{5x+2y=10}\\{2x+5y=8}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
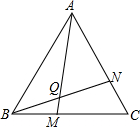 学完“轴对称”这一章后,老师布置了一道思考题:如图所示,点M、N分别在等边△ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求证:∠BQM=60°
学完“轴对称”这一章后,老师布置了一道思考题:如图所示,点M、N分别在等边△ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求证:∠BQM=60°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲乙两城市之间有一条公路相连,公路中途穿过丙市,现有两位司机M、N相约各自同时从甲乙两地出发,途中M将一件物品交给N,已知M从甲市到丙市,N从乙市到甲市,N的速度是M的0.75,他们开车距离丙市的距离y(千米)与行驶的时间t(小时)的函数图象如图所示.
甲乙两城市之间有一条公路相连,公路中途穿过丙市,现有两位司机M、N相约各自同时从甲乙两地出发,途中M将一件物品交给N,已知M从甲市到丙市,N从乙市到甲市,N的速度是M的0.75,他们开车距离丙市的距离y(千米)与行驶的时间t(小时)的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com