练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    用长度一定的绳子围成一个矩形，如果矩形的一边长x（m）与面积y（m2）满足函数关系y=-（x-12）2+144（0＜x＜24），则该矩形面积的最大值为    m2．
    【答案】分析：本题考查二次函数最大（小）值的求法．
    解答：解：由函数关系y=-（x-12）2+144（0＜x＜24）可知，
    ∵二次函数的二次项系数即-1＜0，
    ∴当x=12时，y最大值=144．
    点评：求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法，当二次系数a的绝对值是较小的整数时，用配方法较好，如y=-x2-2x+5，y=3x2-6x+1等用配方法求解比较简单．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    10、用长度一定的绳子围成一个矩形，如果矩形的一边长x（m）与面积y（m2）满足函数关系y=-（x-12）2+144（0＜x＜24），则该矩形面积的最大值为
    144
    m2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    .用长度一定的绳子围成一个矩形，如果矩形的一边长x(m)与面积y(m)满足函数关系y=-(x-12)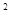+144（0<x<24），则该矩形面积的最大值为_____________.

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

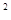    .用长度一定的绳子围成一个矩形，如果矩形的一边长x(m)与面积y(m)满足函数关系y=-(x-12)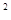+144（0<x<24），则该矩形面积的最大值为_____________.

    查看答案和解析>>

    科目：初中数学 来源：湖北省双峰县2012届九年级下学期期末考试数学卷 题型：选择题

    .用长度一定的绳子围成一个矩形，如果矩形的一边长x(m)与面积y(m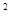)满足函数关系y=-(x-12)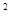+144（0<x<24），则该矩形面积的最大值为_____________.

     

    查看答案和解析>>

    科目：初中数学 来源：第2章《二次函数》常考题集（15）：2.6 何时获得最大利润（解析版） 题型：填空题

    用长度一定的绳子围成一个矩形，如果矩形的一边长x（m）与面积y（m2）满足函数关系y=-（x-12）2+144（0＜x＜24），则该矩形面积的最大值为    m2．

    查看答案和解析>>

    同步练习册答案