
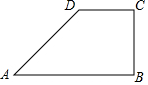
 如图,四边形ABCD中,AB||CD,BC⊥AB;AD=5,CD=3,BC=4.
如图,四边形ABCD中,AB||CD,BC⊥AB;AD=5,CD=3,BC=4.分析 (1)以直线AB为x轴,直线BC为y轴,点B为原点(O)建立直角坐标系,根据CD、BC的长度即可找出点B、C、D的坐标,过点D作DE⊥AB于点E,利用勾股定理即可求出AE的长度,结合BE=CD即可找出点A的坐标;
(2)取线段CD的中点M,线段AD的中点N,根据点A、D、C的坐标即可求出点M、N的坐标.
解答 解:(1)以直线AB为x轴,直线BC为y轴,点B为原点(O)建立直角坐标系,如图所示.
∵CD=3,BC=4,
∴点B(0,0),点C(0,4),点D(-3,4).
过点D作DE⊥AB于点E,则DE=BC=4,
∵AD=5,DE=4,
∴AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=3,
∴AB=AE+BE=3+3=6,
∴点A(-6,0).
(2)取线段CD的中点M,线段AD的中点N,
∵C(0,4),D(-3,4),A(-6,0),
∴点M(-$\frac{3}{2}$,4),点N(-$\frac{9}{2}$,2).
点评 本题考查了勾股定理以及坐标与图形的性质,解题的关键是:(1)建立合适的直角坐标系;(2)根据点A、D、C的坐标求出点M、N的坐标.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 钝角三角形 | C. | 锐角三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
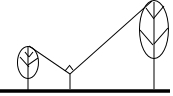 如图,身高1.5米的人站在两棵树之间,距较高的树5米,距较矮的树3米,若此人观察的树梢所成的视线的夹角是90°,且较矮的树高4米,那么较高的树有多少米?
如图,身高1.5米的人站在两棵树之间,距较高的树5米,距较矮的树3米,若此人观察的树梢所成的视线的夹角是90°,且较矮的树高4米,那么较高的树有多少米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一定不相似 | B. | 不一定相似 | C. | 一定相似 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知长度分别为2,4,x的三条线段可以组成一个三角形,且x为正整数.
已知长度分别为2,4,x的三条线段可以组成一个三角形,且x为正整数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,C、D在⊙O上,D是弧AC的中点,过点D作DE⊥BC于点E,并交BA延长线于点F,若AB=9,CE=1,则AD的长为( )
如图,AB是⊙O的直径,C、D在⊙O上,D是弧AC的中点,过点D作DE⊥BC于点E,并交BA延长线于点F,若AB=9,CE=1,则AD的长为( )| A. | 2 | B. | 2.4 | C. | 3 | D. | 3.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com