
【题目】已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、 D. 求证:PC=PD.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】符合下列条件之一的四边形不一定是菱形的是( )
A. 四条边相等
B. 两组邻边分别相等
C. 对角线相互垂直平分
D. 两条对角线分别平分一组对角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,在△ABC和△ADE中,AB=AC=AD=AE,当∠BAC+∠DAE=180°时,我们称△ABC与△DAE互为“顶补等腰三角形”,△ABC的边BC上的高线AM叫做△ADE的“顶心距”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△ABC与△DAE互为“顶补三角形”,AM,AN是“顶心距”.
①如图2,当∠BAC=90°时,AM与DE之间的数量关系为AM= DE;
②如图3,当∠BAC=120°,BC=6时,AN的长为 .
猜想论证:
(2)在图1中,当∠BAC为任意角时,猜想AM与DE之间的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形ABCD,AD=AB,CD=BC,∠B=90°,∠A=60°,CD=2,在四边形ABCD的内部是否存在点P,使得△PAD与△PBC互为“顶补等腰三角形”?若存在,请给予证明,并求△PBC的“顶心距”的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).

(1)当点Q在边AC上时,正方形DEFQ的边长为 cm(用含x的代数式表示);
(2)当点P不与点B重合时,求点F落在边BC上时x的值;
(3)当0<x<2时,求y关于x的函数解析式;
(4)直接写出边BC的中点落在正方形DEFQ内部时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
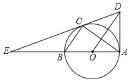
【题目】如图,AB是⊙O直径,C是半圆上一点,连接BC、AC,过点O作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AE=3,CE=![]() ,求线段CE、BE与劣弧BC所围成的图形面积(结果保留根号和π).
,求线段CE、BE与劣弧BC所围成的图形面积(结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
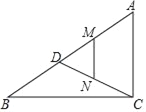
【题目】如图,在Rt△ABC 中,∠ACB=90°,AC=6,BC=8,点D是线段AB上的动点,M、N分别是AD、CD的中点,连接MN,当点D由点A向点B运动的过程中,线段MN所扫过的区域的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
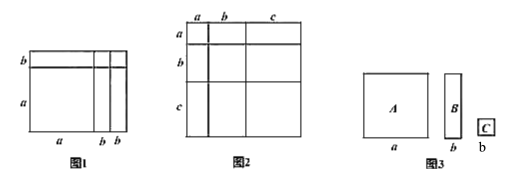
【题目】我们知道:有些代数恒等式可以利用平面图形的面积来表示,如:
![]() 就可以用如图所示的面积关系来说明。
就可以用如图所示的面积关系来说明。
(1)请根据如图写出代数恒等式,并根据所写恒等式计算:![]()
(2)若![]() 求
求![]() 的值;
的值;
(3)现有如图中的彩色卡片:A型、B型、C型,把这些卡片不重叠不留缝隙地贴在棱长为![]() 的100个立方体表面进行装饰,A型、B型、C型卡片的单价分别为0.7元/张、0.5元/张、0.4元/张,共需多少费用?
的100个立方体表面进行装饰,A型、B型、C型卡片的单价分别为0.7元/张、0.5元/张、0.4元/张,共需多少费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在7×7网格中,每个小正方形的边长都为1.

(1)若点A(1,3),C(2,1), ①建立适当的平面直角坐标系;②点B的坐标为( , );
(2)判断△ABC的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com