
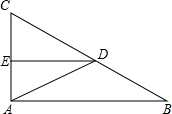
 如图所示,在△ABC中,∠BAC=90°,D为BC的中点,DE⊥AC于点E,∠ADB=2∠ADC,求∠ADE的度数.
如图所示,在△ABC中,∠BAC=90°,D为BC的中点,DE⊥AC于点E,∠ADB=2∠ADC,求∠ADE的度数. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 3a-1 | 2a+5b |
| a-2b+8 |
| A、a=1,b=1 |
| B、a=2,b=-1 |
| C、a=-2,b=1 |
| D、a=-1,b=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
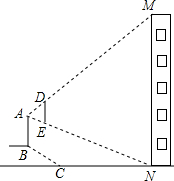 如图,小明家居住的家属楼前20米处有一土丘,经测量斜坡长为8米,坡角恰好为30°.一天小明站在斜坡顶端B处,手持1米的木棒ED(手臂长为0.6米,手臂与身子垂直,木棒与身子平行),发现眼睛A、木棒的顶端D、楼房的顶端M在一条直线上;眼睛A、木棒的底端E、楼房的底部N三点共线,请你计算小明家居住的这栋楼的高度.(结果精确到1米,
如图,小明家居住的家属楼前20米处有一土丘,经测量斜坡长为8米,坡角恰好为30°.一天小明站在斜坡顶端B处,手持1米的木棒ED(手臂长为0.6米,手臂与身子垂直,木棒与身子平行),发现眼睛A、木棒的顶端D、楼房的顶端M在一条直线上;眼睛A、木棒的底端E、楼房的底部N三点共线,请你计算小明家居住的这栋楼的高度.(结果精确到1米,| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com