
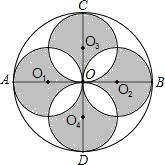
 如图,AB、CD是⊙O的两条互相垂直的直径,点O1、O2、O3、O4分别OA、OB、OC、OD的中点,若⊙O的半径是4,则阴影部分的面积为32.
如图,AB、CD是⊙O的两条互相垂直的直径,点O1、O2、O3、O4分别OA、OB、OC、OD的中点,若⊙O的半径是4,则阴影部分的面积为32. 分析 首先根据已知得出正方形内空白面积,进而得出扇形COB中两空白面积相等,进而得出阴影部分面积.
解答 解:如图所示:连接EFMN,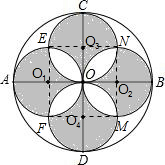
∵四边形的边长为4,四个角都是直角,
∴四边形EFMN是正方形,
正方形中两部分阴影面积为:42-π×22=16-4π,
∴正方形内空白面积为:16-2(16-4π)=8π-16,
∵⊙O的半径为4,
∴O1,O2,O3,O4的半径为2,
∴小圆的面积为:π×22=4π,
扇形COB的面积为:$\frac{90π×{4}^{2}}{360}$=4π,
∴扇形COB中两空白面积相等,
∴阴影部分的面积为:π×42-2(8π-16)=32.
故答案为:32.
点评 此题主要考查了扇形的面积公式以及正方形面积公式,根据已知得出空白面积是解题关键.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
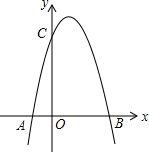 如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(-1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.
如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(-1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
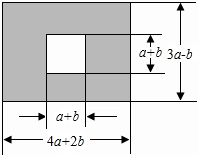 眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a-b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.
眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a-b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
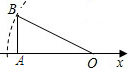 如图,在Rt△OAB中OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,斜边OB的长为半径画弧,交负半轴于一点,则这个点表示的实数是( )
如图,在Rt△OAB中OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,斜边OB的长为半径画弧,交负半轴于一点,则这个点表示的实数是( )| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | -2 | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,现有一圆心角为90°、半径为80cm的扇形铁片,用它恰好围成一个圆锥形的量筒;如果用其它铁片再做一个圆形盖子把量筒底面密封.(接缝都忽略不计).
如图所示,现有一圆心角为90°、半径为80cm的扇形铁片,用它恰好围成一个圆锥形的量筒;如果用其它铁片再做一个圆形盖子把量筒底面密封.(接缝都忽略不计).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com