
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -$\frac{7}{2}$ | 0 | $\frac{5}{2}$ | 4 | $\frac{9}{2}$ | 4 | m | 0 | … |
分析 (1)待定系数法求解可得;
(2)将x=1代入解析式求得y的值,即可得答案.
解答 解:(1)设这个二次函数的表达式为y=a(x-h)2+k.
依题意可知,顶点(-1,$\frac{9}{2}$),
∴$y=a{(x+1)^2}+\frac{9}{2}$.
∵(0,4),
∴$4=a{(0+1)^2}+\frac{9}{2}$.
∴$a=-\frac{1}{2}$.
∴这个二次函数的表达式为$y=-\frac{1}{2}{(x+1)^2}+\frac{9}{2}$.
(2)当x=1时,y=-$\frac{1}{2}$×4+$\frac{9}{2}$=$\frac{5}{2}$,
即$m=\frac{5}{2}$.
点评 本题主要考查待定系数法求函数的解析式,在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
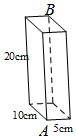 如图,长方体的长为10cm,宽为5cm,高为20cm.若一只蚂蚁沿着长方体的表面从点A爬到点B,需要爬行的最短路径是( )
如图,长方体的长为10cm,宽为5cm,高为20cm.若一只蚂蚁沿着长方体的表面从点A爬到点B,需要爬行的最短路径是( )| A. | 20+5$\sqrt{5}$ | B. | 25 | C. | 10$\sqrt{5}$+5 | D. | $5\sqrt{21}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
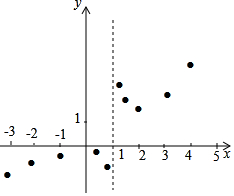 有这样一个问题:探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质.
有这样一个问题:探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质.| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | $\frac{7}{10}$ | $\frac{13}{10}$ | $\frac{3}{2}$ | 2 | 3 | 4 | … |
| y | … | -$\frac{9}{8}$ | -$\frac{2}{3}$ | -$\frac{1}{4}$ | 0 | -$\frac{1}{4}$ | -$\frac{49}{60}$ | $\frac{169}{60}$ | $\frac{9}{4}$ | 2 | m | $\frac{8}{3}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有一个内角大于60° | B. | 有一个内角小于60° | ||
| C. | 每一个内角都大于60° | D. | 每一个内角都小于60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com