
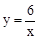 ��x��
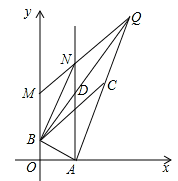
��x�� ��ͼ����һ��P��PA��x���ڵ�A��a��0������B����Ϊ��0��b����b��0��������M��y����������B���Ϸ��ĵ㣬����N������AP�ϣ�����B��AB�Ĵ��ߣ�������AP�ڵ�D����ֱ��MN�ڵ�Q������AQ��ȡAQ���е�ΪC��
��ͼ����һ��P��PA��x���ڵ�A��a��0������B����Ϊ��0��b����b��0��������M��y����������B���Ϸ��ĵ㣬����N������AP�ϣ�����B��AB�Ĵ��ߣ�������AP�ڵ�D����ֱ��MN�ڵ�Q������AQ��ȡAQ���е�ΪC��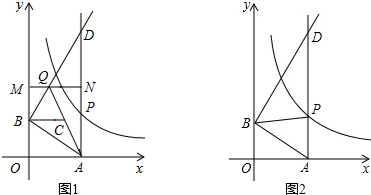
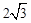 �����ʱP������ꣻ
�����ʱP������ꣻ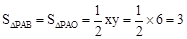 ��
��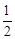 AQ�����BQC=60�㣬��BAQ=30�㡣
AQ�����BQC=60�㣬��BAQ=30�㡣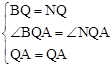 �����ABQ�ա�ANQ��SAS����
�����ABQ�ա�ANQ��SAS����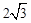 ����BQ=2����AB=
����BQ=2����AB=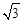 BQ=
BQ=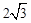 ����OA=
����OA=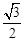 AB=3��
AB=3��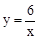 ��ͼ���ϣ���P������Ϊ��3��2����
��ͼ���ϣ���P������Ϊ��3��2����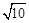 ��
��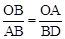 ����BD=3
����BD=3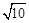 ��
��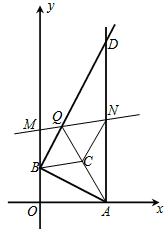
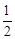 AQ��
AQ��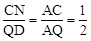 ����BQ=CN=
����BQ=CN=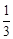 BD=
BD=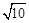 ��
��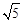 ��
��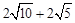 ��
��
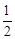 AQ��
AQ��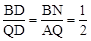 ����BQ=3BD=9
����BQ=3BD=9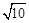 ��
��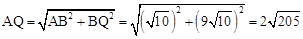 ��
��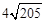 ��
��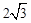 ���OA=3������P�����������
���OA=3������P�����������


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��x��0������D�㣬����D��DC��x�ᣬ����ΪG������OD����֪��AOB�ա�ACD��
��x��0������D�㣬����D��DC��x�ᣬ����ΪG������OD����֪��AOB�ա�ACD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ��ͼ���ϵ�һ��,AB��x���ڵ�B,�ҡ�ABO�������3,��k��ֵ��( )
��ͼ���ϵ�һ��,AB��x���ڵ�B,�ҡ�ABO�������3,��k��ֵ��( )
| A��3 | B����3 | C����6 | D��6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
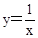 ��x��0����ͼ���ϣ���P1OA1����P2A1A2����P3A2A3��������PnAn��1An���ǵ���ֱ�������Σ�б��OA1��A1A2��A2A3������An��1An����x���ϣ�n�Ǵ��ڻ����2���������������P3��������������������Pn���������������������ú�n��ʽ�ӱ�ʾ����
��x��0����ͼ���ϣ���P1OA1����P2A1A2����P3A2A3��������PnAn��1An���ǵ���ֱ�������Σ�б��OA1��A1A2��A2A3������An��1An����x���ϣ�n�Ǵ��ڻ����2���������������P3��������������������Pn���������������������ú�n��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
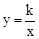 ��һ����������Ϊ��3��4���������ǵ���һ������������
��һ����������Ϊ��3��4���������ǵ���һ������������
| A������3��4�� | B������4����3�� | C������3����4�� | D����4��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ����������ͬ�ĵ�A��m��n����m��2����B��p��q����ֱ��y=��x+m+n��y�ύ�ڵ�C�����OBC�����S��ȡֵ��Χ��
����������ͬ�ĵ�A��m��n����m��2����B��p��q����ֱ��y=��x+m+n��y�ύ�ڵ�C�����OBC�����S��ȡֵ��Χ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com