
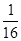 x2-
x2-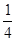 x-6(2) (3)见解析
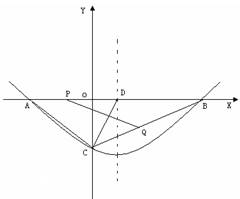
x-6(2) (3)见解析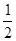 AC,再求出AP,然后根据时间=路程÷速度求出点P运动的时间t,根据勾股定理求出BC,然后求出CQ,根据速度=路程÷时间,计算即可求出点Q的速度.(3)假设存在这样的点M,使得△MPQ为等腰三角形,那么就需要要分类讨论:①当MP=MQ,即M为顶点;②;当PQ为等腰△MPQ的腰时,且P为顶点;③当PQ为等腰△MPQ的腰时,且Q为顶点.进行分类求解即可.
AC,再求出AP,然后根据时间=路程÷速度求出点P运动的时间t,根据勾股定理求出BC,然后求出CQ,根据速度=路程÷时间,计算即可求出点Q的速度.(3)假设存在这样的点M,使得△MPQ为等腰三角形,那么就需要要分类讨论:①当MP=MQ,即M为顶点;②;当PQ为等腰△MPQ的腰时,且P为顶点;③当PQ为等腰△MPQ的腰时,且Q为顶点.进行分类求解即可.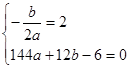 ,解得:a=
,解得:a=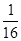 ,b=-
,b=-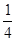
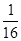 x2-
x2-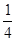 x-6;
x-6;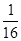
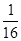 x2-
x2-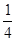 x-6.
x-6.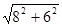 =10=AD
=10=AD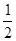 AC=5.
AC=5.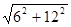 =6
=6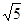 ∴CQ=3
∴CQ=3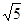
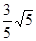 单位长度.
单位长度. 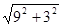 =3
=3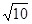 .
.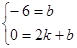 ,解得:
,解得: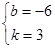 .
.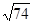
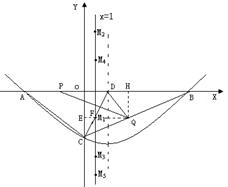
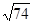 ) M3(1,-
) M3(1,-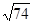 ).
).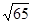
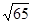 ) M5((1, -3-
) M5((1, -3-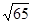 ) .
) .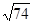 ), M3(1,-
), M3(1,-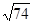 ), M4(1, -3+
), M4(1, -3+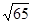 ),
),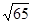 )
)


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源:不详 题型:解答题
 )为圆心,以2为半径的圆与
)为圆心,以2为半径的圆与 轴交于A、B两点.
轴交于A、B两点.
 的图象经过点A、B,试确定此二次函数的解析式.
的图象经过点A、B,试确定此二次函数的解析式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
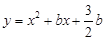 的图象与x轴交于A、B两点(B在A的左侧),顶点为C, 点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
的图象与x轴交于A、B两点(B在A的左侧),顶点为C, 点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
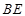 .求证:
.求证: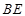 平分
平分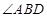 ;
;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=(x﹣1)2+3 | B.y=(x+1)2+3 |
| C.y=(x﹣1)2﹣3 | D.y=(x+1)2﹣3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
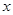 轴的交点为(x1,0)和(2,0),且-2<x1<-1,则下列结论正确的是( )
轴的交点为(x1,0)和(2,0),且-2<x1<-1,则下列结论正确的是( )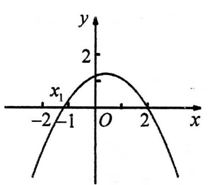
A.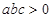 | B.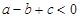 | C.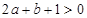 | D.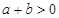 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com