
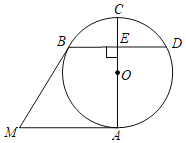
【题目】如图,⊙O中,AC为直径,MA,MB分别切⊙O于点A,B,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,则∠AMB的大小为_____度.
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
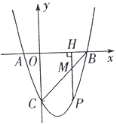
【题目】如图,二次函数y=ax2+bx-3的图象与x轴相交于A(-1,0),B(3,0)两点.与y轴相交于点C
(1)求这个二次函数的解析式.
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,请问:当点P的坐标为多少时,线段PM的长最大?并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用1200元购进一批甲玩具,用800元购进一批乙玩具,所购甲玩具件数是乙玩具件数的![]() ,已知甲玩具的进货单价比乙玩具的进货单价多1元.
,已知甲玩具的进货单价比乙玩具的进货单价多1元.
(1)求:甲、乙玩具的进货单价各是多少元?
(2)玩具售完后,超市决定再次购进甲、乙玩具(甲、乙玩具的进货单价不变),购进乙玩具的件数比甲玩具件数的2倍多60件,求:该超市用不超过2100元最多可以采购甲玩具多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形OABC在平面直角坐标系中,点A,C分别在x轴,y轴的正半轴上,等腰直角三角形OEF的直角顶点O在原点,E,F分别在OA,OC上,且OA=4,OE=2.将△OEF绕点O逆时针旋转,得△OE1F1,点E,F旋转后的对应点为E1,F1.
(Ⅰ)①如图①,求E1F1的长;②如图②,连接CF1,AE1,求证△OAE1≌△OCF1;
(Ⅱ)将△OEF绕点O逆时针旋转一周,当OE1∥CF1时,求点E1的坐标(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,![]() 辆大货车与
辆大货车与![]() 辆小火车一次可以运货
辆小火车一次可以运货![]() 吨,
吨,![]() 辆大货车与
辆大货车与![]() 辆小货车一次可以运货
辆小货车一次可以运货![]() 吨.
吨.
(1)求![]() 辆大货车和
辆大货车和![]() 辆小货车一次可以分别运多少吨;
辆小货车一次可以分别运多少吨;
(2)现有![]() 吨货物需要运输,货运公司拟安排大小货车共
吨货物需要运输,货运公司拟安排大小货车共![]() 辆把全部货物一次运完.求至少需要安排几辆大货车?
辆把全部货物一次运完.求至少需要安排几辆大货车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郑州市某中学体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为1.6米,现要做一个不锈钢的扶手![]() 及两根与
及两根与![]() 垂直且长为1米的不锈钢架杆
垂直且长为1米的不锈钢架杆![]() 和
和![]() (杆子的底端分别为
(杆子的底端分别为![]() ),且
),且![]() ,求所用不锈钢材料的总长度.(即
,求所用不锈钢材料的总长度.(即![]() ,结果精确到0.1米)参考数据(
,结果精确到0.1米)参考数据(![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程.
已知:四边形![]() 是平行四边形.
是平行四边形.
求作:菱形![]() (点
(点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上).
上).
作法:①以![]() 为圆心,
为圆心,![]() 长为半径作弧,交
长为半径作弧,交![]() 于点
于点![]() ;
;
②以![]() 为圆心,
为圆心,![]() 长为半径作弧,交
长为半径作弧,交![]() 于点
于点![]() ;
;
③连接![]() .所以四边形
.所以四边形![]() 为所求作的菱形.
为所求作的菱形.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() ,
,![]() ,
,
∴ = .
在![]() 中,
中,![]() .
.
即![]() .
.
∴四边形![]() 为平行四边形.
为平行四边形.
∵![]() ,
,
∴四边形![]() 为菱形( )(填推理的依据).
为菱形( )(填推理的依据).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com