练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知O是四边形ABCD内一点，OA＝OB＝OC，∠ABC＝∠ADC＝70°，则∠DAO＋∠DCO的大小是________．

    【答案】150°

    【解析】

    首先由OA=OB=OC，得出∠OAB+∠OBA+∠OBC+∠OCB=140°，进而由四边形内角和定理得出，∠OAB+∠ABC+∠OCB=140°，再利用四边形内角和从而可得出答案．

    解：∵OA=OB=OC，


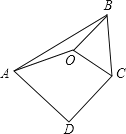
    ∴∠OAB=∠OBA，∠OBC=∠OCB，
    ∵∠ABC=∠OBA+∠OBC=70°，
    ∴∠OAB+∠OBA+∠OBC+∠OCB=140°，即∠OAB+∠ABC+∠OCB=140°，
    又∵∠ABC+∠BCD+∠ADC+∠BAD=360°，即∠ABC+∠OCB+∠OCD+∠ADC+∠DAO+∠OAB=360°，
    ∵∠ADC=70°，∠OAB+∠ABC+∠OCB=140°，
    ∴∠DAO+∠DCO=360°-140°-70°=150°．

    故答案为：150°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某商店购买60件A商品和30件B商品共用了1080元，购买50件A商品和20件B商品共用了880元．

    (1) A商品的单价是___________元，B商品的单价是___________元；

    (2) 已知该商店购买B商品的件数比购买A商品的件数的2倍少4件，设购买A商品的件数为x件，该商店购买的A、B两种商品的总费用为y元．

    ① 求y与x的函数关系式．

    ② 如果需要购买A、B两种商品的总件数不少于32件，且该商店购买的A、B两种商品的总费用不超过296元，求购买B商品最多有多少件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点E在AB上，点D在BC上，BD＝BE，∠BAD＝∠BCE，AD与CE相交于点F，试判断△AFC的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校在一次比赛中将所有参赛同学分为四个组，其中第一组有x人，第二组比第一组的少5人，第三组比第一、二组的和少15人，第一组的2倍与第四组的和是30人．

    （1）用含x的式子分别表示第二、三、四组的人数及参赛总人数；

    （2）当x＝10时，第四组与第三组相比，哪组的人数多？多多少人？

    （3）x能否等于13，为什么？x能否等于20，为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了掌握八年级数学考试卷的命题质量与难度系数，命题组教师赴外地选取一个水平相当的八年级班级进行预测，将考试成绩分布情况进行处理分析，制成频数分布表如下(成绩得分均为整数)：

    组别

    成绩分组

    频数频率

    频数

    1

    2

    0.05

    2

    4

    0.10

    3

    0.2

    4

    10

    0.25

    5

    6

    6

    0.15

    合计

    40

    1.00

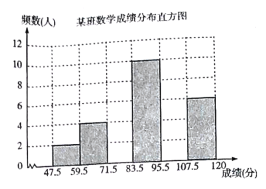
    根据表中提供的信息解答下列问题：

    （1）频数分布表中的 ， ， ；

    （2）已知全区八年级共有200个班(平均每班40人)，用这份试卷检测，108分及以上为优秀，预计优秀的人数约为 ，72分及以上为及格，预计及格的人数约为 ，及格的百分比约为 ；

    （3）补充完整频数分布直方图.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在梯形 ABCD 中，AD∥BC，E 是 AB 的中点，CE 的延长线与 DA 的延长线相 交于点 F．

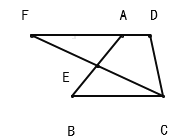
    （1）求证：△BCE≌△AFE；

    （2）连接 AC、FB，则 AC 与 FB 的数量关系是 ，位置关系是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图， AD 为△ ABC 的中线， BE 为△ ABD 的中线．

    （1）∠ ABE=15°，∠ BED=55°，求∠ BAD 的度数；

    （2）作△ BED 的边 BD 边上的高；

    （3）若△ ABC 的面积为 20， BD=2.5，求△ BDE 中 BD 边上的高.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

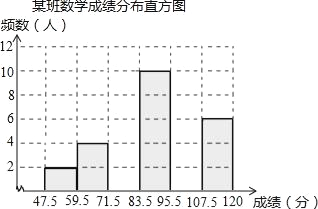
    【题目】为了掌握八年级数学考试卷的命题质量与难度系数，命题组教师赴外地选取一个水平相当的八年级班级进行预测，将考试成绩分布情况进行处理分析，制成频数分布表如下（成绩得分均为整数）：

    组别

    成绩分组

    频数

    频率

    1

    47.5～59.5

    2

    0.05

    2

    59.5～71.5

    4

    0.10

    3

    71.5～83.5

    a

    0.2

    4

    83.5～95.5

    10

    0.25

    5

    95.5～107.5

    b

    c

    6

    107.5～120

    6

    0.15

    合计

    40

    1.00

    根据表中提供的信息解答下列问题：

    （1）频数分布表中的a=__________，b=__________，c=__________；

    （2）已知全区八年级共有200个班（平均每班40人），用这份试卷检测，102018年四川省内江市及以上为优秀，预计优秀的人数约为__________，72分及以上为及格，预计及格的人数约为__________，及格的百分比约为__________；

    （3）补充完整频数分布直方图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在下列生活、生产现象中，可以用基本事实“两点确定一条直线”来解释的是（　　）

    ①用两颗钉子就可以把木条固定在墙上；②把笔尖看成一个点，当这个点运动时便得到一条线；③把弯曲的公路改直，就能缩短路程；④植树时，只要栽下两棵树，就可以把同一行树栽在同一条直线上．

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案