
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式![]() .
.
(1)求a,b,c的值;
(2)如果在第二象限内有一点P(m,![]() ),使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
),使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)a=2,b=3,c=4;(2)P(-3,![]() ).
).
【解析】
(1)用非负数的性质求解可得a,b,c的值;
(2)把四边形ABOP的面积看成两个三角形面积和,用m来表示;依据四边形ABOP的面积与三角形ABC的面积相等,列方程即可.
(1)由已知![]() ,
,
可得:a-2=0,b-3=0,c-4=0,
解得a=2,b=3,c=4;
(2)∵S△ABO=![]() ×2×3=3,S△APO=
×2×3=3,S△APO=![]() ×2×(-m)=-m,
×2×(-m)=-m,
∴S四边形ABOP=S△ABO+S△APO=3+(-m)=3-m;
∵S△ABC=![]() ×4×3=6,
×4×3=6,
又∵S四边形ABOP=S△ABC
∴3-m=6,
解得m=-3,
∴存在点P(-3,![]() )使S四边形ABOP=S△ABC.
)使S四边形ABOP=S△ABC.


科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,花丛中有一路灯杆AB. 在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米. 如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
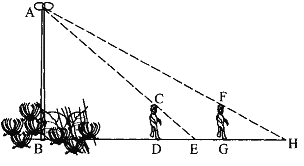
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
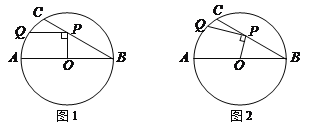
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接三角形ABC中,∠ACB=90°,AC=2BC,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是![]() 上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
(1)求证:△PAC∽△PDF;
(2)若AB=5,![]() ,求PD的长;
,求PD的长;
(3)在点P运动过程中,设![]() =x,tan∠AFD=y,求y与x之间的函数关系式.(不要求写出x的取值范围)
=x,tan∠AFD=y,求y与x之间的函数关系式.(不要求写出x的取值范围)
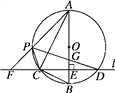
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,第一象限内长方形ABCD,AB∥y轴,点A(1,1),点C(a,b),满足![]() +|b﹣3|=0.
+|b﹣3|=0.
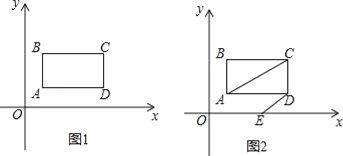
(1)求长方形ABCD的面积.
(2)如图2,长方形ABCD以每秒1个单位长度的速度向右平移,同时点E从原点O出发沿x轴以每秒2个单位长度的速度向右运动,设运动时间为t秒.
①当t=4时,直接写出三角形OAC的面积为 ;
②若AC∥ED,求t的值;
(3)在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An.
①若点A1的坐标为(3,1),则点A3的坐标为 ,点A2014的坐标为 ;
②若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
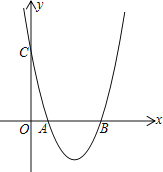
【题目】如图1,抛物线y=x2+bx+c与x轴交于A(1,0)、B(4,0),与y轴交于点C
(1) 求抛物线的解析式
(2) 抛物线上一点D,满足S△DAC=S△OAC,求点D的坐标
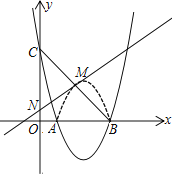
(3) 如图2,已知N(0,1),将抛物线在点A、B之间部分(含点A、B)沿x轴向上翻折,得到图T(虚线部分),点M为图象T的顶点.现将图象保持其顶点在直线MN上平移,得到的图象T1与线段BC至少有一个交点,求图象T1的顶点横坐标的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,把下面的推理过程补充完整,并在括号内注明理由:
如图,已知A、B、C、D在同一直线上,AE∥DF,AC=BD,∠E=∠F,求证:BE∥CF.

证明:∵AE∥DF(已知)
∴_________(两直线平行,内错角相等)
∵AC=BD(已知)
又∵AC=AB+BC,BD=BC+CD
∴________(等式的性质)
∵∠E=∠F(已知)
∴△ABE≌△DCF(___________)
∴∠ABE=∠DCF(_________________)
∵ABF+∠CBE=180°,∠DCF+∠BCF=180°
∴∠CBE=∠BCF(__________________)
∴BE∥CF(________________________)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com