练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．如图，数轴上的点A所表示的数为a，化简|a|+|1-a|的结果为（　　）
    A．1B．2a-1C．2a+1D．1-2a

    分析 根据数轴上点的位置判断出绝对值里边式子的正负，利用绝对值的代数意义化简，合并即可得到结果．

    解答 解：根据数轴上点的位置得：1＜a＜2，
    ∴1-a＜0，
    则原式=a+a-1=2a-1，
    故选B

    点评 此题考查了整式的加减，数轴，以及绝对值，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    4．单项式-$\frac{2abc}{3}$的系数和次数分别是（　　）
    A．-$\frac{2}{3}$，3B．-$\frac{2}{3}$，1C．-2，3D．-2，1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

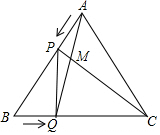    5．如图，边长为4cm的等边△ABC中，点P、Q分别是边AB、BC上的动点（端点除外），点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，连接AQ，CP交于点M，在点P，Q运动的过程中．
    （1）求证：△ABQ≌△CAP；
    （2）∠QMC的大小是否发生变化？若无变化，求∠QMC的度数；若有变化，请说明理由；
    （3）连接PQ，当点P，Q运动多少秒时，△PBQ是直角三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．从3，-1，$\frac{1}{2}$，1，-3这5个数中，随机抽取一个数记为a，若数a使关于x的不等式组$\left\{\begin{array}{l}{\frac{1}{3}（2x+7）≥3}\\{x-a＜0}\end{array}\right.$无解，且使关于x的分式方程$\frac{x}{x-3}$-$\frac{a-2}{3-x}$=-1有整数解，那么这5个数中所有满足条件的a的值之积是（　　）
    A．$\frac{1}{2}$B．3C．-3D．-$\frac{3}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图，C，D是以线段AB为直径的⊙O上两点，若CA=CD，且∠ACD=30°，则∠CAB=（　　）
    A．15°B．20°C．25°D．30°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．（1）如图（1），在△ABC和△CDE中，已知AC⊥BC，EC⊥DC，且AC=CD，BC=CE，你能判断AB与ED的关系吗？
    （2）若将△ABC沿CD方向平移得到图（2），请直接判断△ADE的形状，不需要说明理由；若此时EC1=7，AC2=3，你知道线段C1C2的长度吗？说明你的解题思路．
    （3）应用上述方法与结论，按照图（3）中的数据，请你直接写出图（3）中实线所围成的图形面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列由左到右的变形，属于因式分解的是（　　）
    A．（x+2）（x-2）=x2-4B．x2-4=（x+2）（x-2）
    C．x2-4+3x=（x+2）（x-2）+3xD．x2+4x-2=x（x+4）-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，在△ABC中，∠ACB=Rt∠，BC=6，AC=8，点D是AC的中点，点P为AB边上的动点（P不与A重合），AP=t（t＞0），PH⊥AC于点H，则PH=$\frac{3}{5}$t，连结DP并延长至点E，使得PE=PD，作点E关于AB的对称点F，连结FH
    （1）用t的代数式表示DH的长；
    （2）求证：DF∥AB；
    （3）若△DFH为等腰三角形，求t（0＜t≤5）的值．（提示：以∠A为较小锐角的直角三角形的三边比为3：4：5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．二次函数y=ax2+bx和反比例函数y=$\frac{b}{x}$在同一直角坐标系中的大致图象是（　　）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案