Question

【题目】白色污染（White Pollution）是人们对难降解的塑料垃圾（多指塑料袋）污染环境现象的一种形象称谓.为了让全校同学感受丢弃塑料袋对环境的影响，小彬随机抽取某小区户居民，记录了这些家庭年某个月丢弃塑料袋的数量（单位：个）：

请根据上述数据，解答以下问题：

(1)小彬按“组距为”列出了如下的频数分布表（每组数据含最小值），请将表中空缺的部分补充完整，并补全频数直方图；

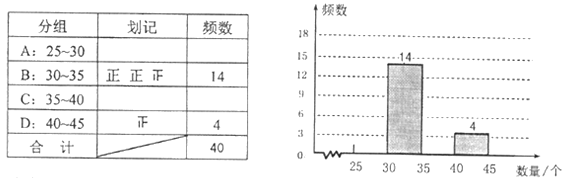
(2)根据(1)中的直方图可以看出，这户居民家这个月丢弃塑料袋的个数在 组的家庭最多；（填分组序号）

(3)根据频数分布表，小彬又画出了右图所示的扇形统计图.请将统计图中各组占总数的百分比填在图中，并求出组对应的扇形圆心角的度数；

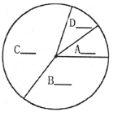
(4)若小区共有户居民家庭，请你估计每月丢弃的塑料袋数量不小于个家庭个数.

Answer 1

【答案】（1）见解析（2）C（3）162°（4）900个

【解析】

（1）根据数据即可补全表格与直方图；（2）由图可知C组的家庭最多；（3）

分别算出各组的占比，再用C组占比乘以360°即可求出圆心角度数；（4）先求出不小于个家庭的占比，再乘以1000即可.

（1）补全表格与直方图如下图：

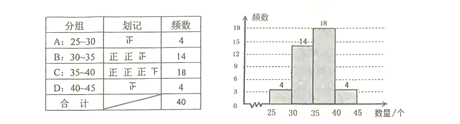
（2）由直方图可知这个月丢弃塑料袋的个数在C组的家庭最多；

（3）A组占比为：，

B组占比为：，

C组占比为：，圆心角度数为360°×45%=162°，

A组占比为：，

补全扇形统计图为

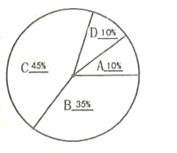
（4）不小于个家庭的占比为35%+45%+10%=90%，

故小区每月丢弃的塑料袋数量不小于个家庭个数为1000×90%=900个.