
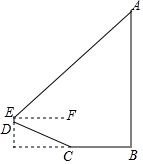
 位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)| A. | 22.5 米 | B. | 24.0 米 | C. | 28.0 米 | D. | 33.3 米 |
分析 过点E作EM⊥AB与点M,根据斜坡CD的坡度(或坡比)i=1:2.4可设CD=x,则CG=2.4x,利用勾股定理求出x的值,进而可得出CG与DG的长,故可得出EG的长.由矩形的判定定理得出四边形EGBM是矩形,故可得出EM=BG,BM=EG,再由锐角三角函数的定义求出AM的长,进而可得出结论.
解答 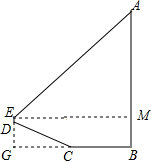 解:过点E作EM⊥AB与点M,
解:过点E作EM⊥AB与点M,
∵斜坡CD的坡度(或坡比)i=1:2.4,BC=CD=13米,
∴设CD=x,则CG=2.4x.
在Rt△CDG中,
∵DG2+CG2=DC2,即x2+(2.4x)2=132,解得x=5,
∴DG=5米,CG=12米,
∴EG=5+0.5=5.5米,BG=13+12=25米.
∵EM⊥AB,AB⊥BG,EG⊥BG,
∴四边形EGBM是矩形,
∴EM=BG=25米,BM=EG=5.5米.
在Rt△AEM中,
∵∠AEM=42°,
∴AM=EM•tan42°≈25×0.90=22.5米,
∴AB=AM+BM=22.5+5.5=28米.
故选C.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1.239×10-3 | B. | 1.239×10-2 | C. | 0.1239×10-2 | D. | 12.39×10-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥-2且x≠1 | B. | x>-2且x≠1 | C. | x≥-2 | D. | x>-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查一批电脑的使用寿命情况 | |
| B. | 调查全国足球迷的身体健康状况 | |
| C. | 调查重庆市中小学生课外阅读情况 | |
| D. | 为保证“神州十一号”载人飞船的成功发射,对其零部件的检查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正数 | B. | 负数 | C. | 零 | D. | 非负数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC三个顶点分别在反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$的图象上,若∠C=90°,AC∥y轴,BC∥x轴,S△ABC=8,则k的值为( )
如图,△ABC三个顶点分别在反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$的图象上,若∠C=90°,AC∥y轴,BC∥x轴,S△ABC=8,则k的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com