
 如图,在?ABCD中,AE⊥BC于点E点,延长BC至F点使CF=BE,连接AF,DE,DF.
如图,在?ABCD中,AE⊥BC于点E点,延长BC至F点使CF=BE,连接AF,DE,DF.分析 (1)先证明四边形AEFD是平行四边形,再证明∠AEF=90°即可.
(2)证明△ABF是直角三角形,由三角形的面积即可得出AE的长.
解答 (1)证明:∵CF=BE,
∴CF+EC=BE+EC.
即 EF=BC.
∵在?ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形.
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD是矩形;
(2)解:∵四边形AEFD是矩形,DE=8,
∴AF=DE=8.
∵AB=6,BF=10,
∴AB2+AF2=62+82=100=BF2.
∴∠BAF=90°.
∵AE⊥BF,
∴△ABF的面积=$\frac{1}{2}$AB•AF=$\frac{1}{2}$BF•AE.
∴AE=$\frac{AB•AF}{BF}$=$\frac{6×8}{10}$=$\frac{24}{5}$.
点评 本题考查矩形的性质、菱形的性质、平行四边形的性质等知识,解题的关键是熟练掌握这些知识的应用,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
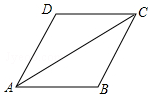 如图,AC是平行四边形ABCD的对角线,∠BAC=∠DAC.
如图,AC是平行四边形ABCD的对角线,∠BAC=∠DAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
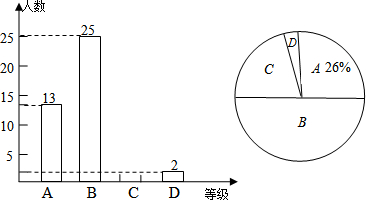
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
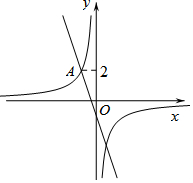 如图,在平面直角坐标系xOy中,直线y=-3x+m与双曲线y=$\frac{k}{x}$相交于点A(m,2).
如图,在平面直角坐标系xOy中,直线y=-3x+m与双曲线y=$\frac{k}{x}$相交于点A(m,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
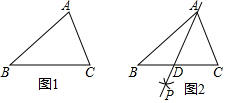 下面是“作三角形一边中线”的尺规作图过程.
下面是“作三角形一边中线”的尺规作图过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:单选题
将一副三角板如图放置,使点在上,则∠AFE的度数为( )

A. 45° B. 50° C. 60° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 选取一个班级的学生 | B. | 选取50名男生 | ||
| C. | 选取50名女生 | D. | 在该校各年级中随机选取50名学生 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com