
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8,tan∠CAD=![]() ,CA=CD,E、F分别是AD、AC上的动点(点E与A、D不重合),且∠FEC=∠ACB.
,CA=CD,E、F分别是AD、AC上的动点(点E与A、D不重合),且∠FEC=∠ACB.
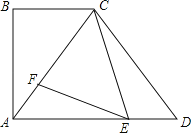
(1)求CD的长;
(2)若AF=2,求DE的长.
【答案】(1)CD=10;(2)DE=2或10.
【解析】
(1)由AD∥BC,可得∠CAD的正弦值,在直角三角形ACB中可求得到AC,从而求得CD的长度;
(2)作CM⊥AD于点M.利用两角对应相等求得三角形AEF与三角形DCE相似,利用其性质可求DE的长.
(1)∵AD∥BC,
∴∠CAD=∠ACB,
又∵∠B=90°,tan∠CAD=![]() ,AB=8,
,AB=8,
∴BC=6,![]() ,
,
∴AC=10,
∴CD=CA=10;
(2)作CM⊥AD于点M.
∵AC=10,![]() ,
,
∴CM=8,
∴AM=6,
∴AD=2AM=12,
∵CA=CD,
∴∠CAD=∠CDA,
又∵∠FEC=∠ACB=∠CAD,
∴∠AFE=∠DEC,
∴△AEF∽△DCE,
∴![]() ,
,
又∵AF=2,BC=6,CD=10,AD=12,
设x=DE,得![]() ,
,
整理解得x=2或x=10,
即DE=2或DE=10.


科目:初中数学 来源: 题型:
【题目】随着城际铁路的开通,从甲市到乙市的高铁里程比快里程缩短了90千米,运行时间减少了8小时,已知甲市到乙市的普快列车里程为1220千米,高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)若从甲市到乙市途经丙市,且从甲市到丙市的高铁里程为780千米.某日王老师要从甲市去丙市参加14:00召开的会议,如果他买了当日10:00从甲市到丙市的高铁票,而且从丙市高铁站到会议地点最多需要0.5小时.试问在高铁列车准点到达的情况下,王老师能否在开会之前赶到会议地点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直径为10的⊙O经过原点O,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长分别是方程x2+kx+48=0的两根.

(1)求线段OA、OB的长;
(2)已知点C在劣弧OA上,连结BC交OA于D,当OC2=CD·CB时,求C点的坐标;
(3)在⊙O上是否存在点P,使S△POD=S△ABD.若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
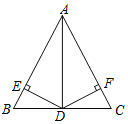
【题目】在△ABC中,AB=AC,点D为边BC上一点,且AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:BE=CF;
(2)若∠B=40°,求∠ADF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
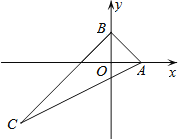
【题目】如图,△ABC在平面直角坐标系中,点A、B分别在x轴和y轴上,且OA=OB,边AC所在直线解析式为y=![]() x﹣
x﹣![]() ,若△ABC的内心在y轴上,则tan∠ACB的值为( )
,若△ABC的内心在y轴上,则tan∠ACB的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 .
(1)EF=![]() OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=![]() OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(5)OGBD=AE2+CF2.
;(5)OGBD=AE2+CF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c 如图所示,直线x=-1是其对称轴,

(1)确定a,b,c, Δ=b2-4ac的符号,
(2)求证:a-b+c>0,
(3)当x取何值时,y>0;当x取何值时y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为激发学生的阅读兴趣,培养学生良好的阅读习惯,我区某校欲购进一批学生喜欢的图书,学校组织学生会随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)填空或选择:此次共调查了______名学生;图2中“小说类”所在扇形的圆心角为______度;学生会采用的调查方式是______.A.普查 B.抽样调查
(2)将条形统计图(图1)补充完整;
(3)若该校共有学生2500人,试估计该校喜欢“社科类”书籍的学生人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com