
分析 (1)直接根据同分母的分式加减法法则进行计算:分母不变,分子相加减;
(2)把第二项的分母提取负号,化成同分母分式;
(3)通分,公分母为(x+2)(x-2);
(4)把a-b看成是一项,为$\frac{a-b}{1}$,再通分;
(5)前两项先通分,再依次计算即可.
解答 解:(1)$\frac{5a+3b}{a+b}+\frac{3b-4a}{a+b}-\frac{a+3b}{a+b}$,
=$\frac{5a+3b+3b-4a-a-3b}{a+b}$,
=$\frac{3b}{a+b}$;
(2)$\frac{5m-n}{{n}^{2}-mn}+\frac{n}{mn-{n}^{2}}-\frac{3m}{{n}^{2}-mn}$,
=$\frac{5m-n}{{n}^{2}-mn}$-$\frac{n}{{n}^{2}-mn}$-$\frac{3m}{{n}^{2}-mn}$,
=$\frac{5m-n-n-3m}{{n}^{2}-mn}$,
=$\frac{2m-2n}{{n}^{2}-mn}$,
=$\frac{2(m-n)}{n(n-m)}$,
=-$\frac{2}{n}$;
(3)$\frac{1}{x-2}+\frac{4}{{{x^2}-4}}+\frac{x-1}{x+2}$,
=$\frac{x+2}{{x}^{2}-4}$+$\frac{4}{{x}^{2}-4}$+$\frac{(x+1)(x-2)}{{x}^{2}-4}$,
=$\frac{x+2+4+{x}^{2}+x-2}{{x}^{2}-4}$,
=$\frac{{x}^{2}+2x+4}{{x}^{2}-4}$;
(4)$a-b+\frac{{2{b^2}}}{a+b}$,
=$\frac{a-b}{1}$+$\frac{2{b}^{2}}{a+b}$,
=$\frac{{a}^{2}-{b}^{2}+2{b}^{2}}{a+b}$,
=$\frac{{a}^{2}+{b}^{2}}{a+b}$;
(5)$\frac{1}{1-x}+\frac{1}{1+x}+\frac{2}{{1+{x^2}}}+\frac{4}{{1+{x^4}}}$,
=$\frac{1+x+1-x}{1-{x}^{2}}$+$\frac{2}{1+{x}^{2}}$+$\frac{4}{1+{x}^{4}}$,
=$\frac{2}{1-{x}^{2}}$+$\frac{2}{1+{x}^{2}}$+$\frac{4}{1+{x}^{4}}$,
=$\frac{2(1+{x}^{2})+2(1-{x}^{2})}{1-{x}^{4}}$+$\frac{4}{1-{x}^{4}}$,
=$\frac{4}{1-{x}^{4}}$+$\frac{4}{1+{x}^{4}}$,
=$\frac{4(1+{x}^{4})+4(1-{x}^{4})}{1-{x}^{8}}$,
=$\frac{8}{1-{x}^{8}}$.
点评 本题考查了分式的加减混合运算,熟练掌握分式的加减混合运算法则是关键:①同分母的分式相加减,分母不变,把分子相加减.②异分母分式加减法,先通分,把异分母分式的加减就转化为同分母分式的加减.本题因式分解是基础,要熟知平方差公式和完全平方公式.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{36}$=±6 | B. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | C. | $\sqrt{12}$÷$\sqrt{2}$=6 | D. | $\sqrt{\frac{3}{2}}$×$\sqrt{24}$=6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
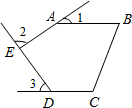 如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=( )
如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=( )| A. | 90° | B. | 180° | C. | 120° | D. | 270° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com