
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y= ![]() (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(1)求一次函数与反比例函数的解析式;
(2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值;
(3)求△ABC的面积.
【答案】
(1)解:∵反比例函数经过点D(﹣2,﹣1),
∴把点D代入y= ![]() (m≠0),
(m≠0),
∴﹣1= ![]() ,
,
∴m=2,
∴反比例函数的解析式为:y= ![]() ,
,
∵点A(1,a)在反比例函数上,
∴把A代入y= ![]() ,得到a=
,得到a= ![]() =2,
=2,
∴A(1,2),
∵一次函数经过A(1,2)、D(﹣2,﹣1),
∴把A、D代入y=kx+b (k≠0),得到: ![]() ,解得:
,解得: ![]() ,
,
∴一次函数的解析式为:y=x+1
(2)解:如图:当﹣2<x<0或x>1时,一次函数的值大于反比例函数的值
(3)解:过点A作AE⊥x轴交x轴于点E,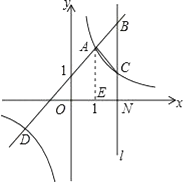
∵直线l⊥x轴,N(3,0),∴设B(3,p),C(3,q),
∵点B在一次函数上,∴p=3+1=4,
∵点C在反比例函数上,∴q= ![]() ,
,
∴S△ABC= ![]() BCEN=
BCEN= ![]() ×(4﹣
×(4﹣ ![]() )×(3﹣1)=
)×(3﹣1)= ![]() .
.
【解析】由反比例函数经过点D(-2,-1),即可求得反比例函数的解析式;然后求得点A的坐标,再利用待定系数法求得一次函数的解析式;
结合图象求解即可求得x在什么范围内,一次函数的值大于反比例函数的值;
首先过点A作AE⊥x轴交x轴于点E,由直线l与x轴垂直于点N(3,0),可求得点E,B,C的坐标,继而求得答案.


科目:初中数学 来源: 题型:
【题目】为了调查市场上某品牌方便面的色素含量是否符合国家标准,工作人员在超市里随机抽取了某品牌的方便面进行检验.图1和图2是根据调查结果绘制的两幅不完整的统计图,其中A、B、C、D分别代表色素含量为0.05%以下、0.05%~0.1%、0.1%~0.15%、0.15%以上,图1的条形图表示的是抽查的方便面中色素含量分布的袋数,图2的扇形图表示的是抽查的方便面中色素的各种含量占抽查总数的百分比.请解答以下问题:

(1)本次调查一共抽查了多少袋方便面?
(2)将图1中色素含量为B的部分补充完整;
(3)图2中的色素含量为D的方便面所占的百分比是多少?
(4)若色素含量超过0.15%即为不合格产品,某超市这种品牌的方便面共有10000袋,那么其中不合格的产品有多少袋?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中折线表示芳芳骑自行车离家的距离与时间的关系,她9点离开家,15点回家,请根据图象回答下列问题:

(1)芳芳到达离家最远的地方时,离家________千米;
(2)第一次休息时离家________ 千米;
(3)她在10:00~10:30的平均速度是_________;
(4)芳芳一共休息了_________ 小时;
(5)芳芳返回用了____________小时;
(6)返回时的平均速度是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(a,0),B(0,2![]() )
)
(1)点(k+1,2k﹣5)关于x轴的对称点在第一象限,a为实数k的范围内的最大整数,求A点的坐标及△AOB的面积;
(2)在(1)的条件下如图1,点P是第一象限内的点,且△ABP是以AB为腰的等腰直角三角形,请直接写出P点坐标;
(3)在(1)的条件下,如图2,以AB、OB的作等边△ABC和等边△OBD,连接AD、OC交于E点,连接BE.
①求证:EB平分∠CED;
②M点是y轴上一动点,求AM+CM最小时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)
(1)画出格点![]() (顶点均在格点上)关于直线
(顶点均在格点上)关于直线![]() 对称的
对称的![]() ;
;
(2)再将![]() 向下平移2单位得
向下平移2单位得![]() ;
;
(3)将![]() 绕点A顺时针旋转90°得
绕点A顺时针旋转90°得![]() ;并求边AB扫过的面积.
;并求边AB扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=-x+1(0≤x≤10)与反比例函数y= ![]() (-10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
(-10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
A.- ![]() ≤x≤1
≤x≤1
B.- ![]() ≤x≤
≤x≤ ![]()
C.- ![]() ≤x≤
≤x≤ ![]()
D.1≤x≤ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【知识链接】 有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.
例如: ![]() 的有理化因式是
的有理化因式是 ![]() ;1﹣
;1﹣ ![]() 的有理化因式是1+
的有理化因式是1+ ![]() .
.
分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到化去分母中根号的目的.如:![]() =
= ![]() =
= ![]() ﹣1,
﹣1, ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() .
.
(1)【知识理解】 填空:2 ![]() 的有理化因式是;
的有理化因式是;
直接写出下列各式分母有理化的结果:
① ![]() =;②
=;② ![]() = .
= .
(2)【启发运用】 计算: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com