

分析 过A作AF⊥BC于F,根据等腰三角形的性质得到BF=CF=$\frac{1}{2}$BC,由AB的垂直平分线交AB于点E,得到BD=AD=4,设DF=x,根据勾股定理列方程即可得到结论.
解答 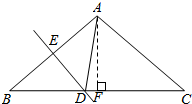 解:过A作AF⊥BC于F,
解:过A作AF⊥BC于F,
∵AB=AC,
∴BF=CF=$\frac{1}{2}$BC,
∵AB的垂直平分线交AB于点E,
∴BD=AD=4,
设DF=x,
∴BF=4+x,
∵AF2=AB2-BF2=AD2-DF2,
即16-x2=36-(4+x)2,
∴x=0.5,
∴DF=0.5,
∴CD=CF+DF=BF+DF=BD+2DF=4+0.5×2=5,
故答案为:5.
点评 此题考查了等腰三角形的性质,线段垂直平分线的性质.此题难度不大,注意掌握转化思想与数形结合思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某超市为了测定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间2分钟到3分钟表示大于或等于2分钟而小于3分钟,其它类同).这个时间段内顾客等待时间不少于6分钟的人数为7.
某超市为了测定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间2分钟到3分钟表示大于或等于2分钟而小于3分钟,其它类同).这个时间段内顾客等待时间不少于6分钟的人数为7.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四边形中至多有一个角是钝角或直角 | |
| B. | 四边形中至少有两个角是钝角或直角 | |
| C. | 四边形中四个角都是钝角或直角 | |
| D. | 四边形中没有一个角是钝角或直角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
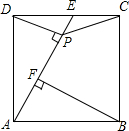 如图,正方形ABCD中,点E为CD的中点,DP⊥AE,垂足为P点,BF⊥AE于F,
如图,正方形ABCD中,点E为CD的中点,DP⊥AE,垂足为P点,BF⊥AE于F,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com