
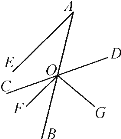
【题目】如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于点O,AE∥OF,且∠A=30°.
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
【答案】(1)∠AOD=60°;(2)见解析.
【解析】
(1)根据两直线平行,同位角相等可得∠FOB=∠A=30![]() ,再根据角平分线的定义求出∠COF=∠FOB=30
,再根据角平分线的定义求出∠COF=∠FOB=30![]() ,然后根据平角等于180
,然后根据平角等于180![]() 列式进行计算即可得解;
列式进行计算即可得解;
(2)先求出∠DOG=60![]() ,再根据对顶角相等求出∠AOD=60
,再根据对顶角相等求出∠AOD=60![]() ,然后根据角平分线的定义即可得解.
,然后根据角平分线的定义即可得解.
解:(1)∵AE∥OF,∴∠BOF=∠A=30°,
∵OF平分∠BOC,∴∠COF=∠BOF=30°,∠DOF=180°-∠COF=150°;
(2)由(1)知∠COF=∠BOF=30°,∴∠BOC=60°,∠AOD=∠BOC=60°,
∵OG⊥OF,∴∠BOG=90°-∠BOF=60°,
∴∠DOG=180°-∠BOC-∠BOG=180°-60°-60°=60°,
∴∠AOD=∠DOG=60°,∴OD平分∠AOG.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
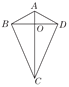
【题目】两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,下列判断正确的有_____(填序号).
①AC⊥BD;②AC,BD互相平分;③AC平分∠BCD;④∠ABC=∠ADC=90°;⑤筝形ABCD的面积为![]() AC·BD.
AC·BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为![]() ,C点的坐标为
,C点的坐标为![]() ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着![]() 的路线移动
的路线移动![]() 即:沿着长方形移动一周
即:沿着长方形移动一周![]() .
.
![]() 写出点B的坐标
写出点B的坐标![]() ______
______![]()
![]() 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
![]() 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根
据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知实数a,b,c满足a+b=ab=c,有下列结论:①若c≠0,则![]() ;②若a=3,则b+c=9;③若c≠0,则(1-a)(1-b)=
;②若a=3,则b+c=9;③若c≠0,则(1-a)(1-b)=![]() ;④若c=5,则a2+b2=15. 其中正确的是( )
;④若c=5,则a2+b2=15. 其中正确的是( )
A. ①③④ B. ①②④ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,∠COD=90°,OE、OF分别是∠COB、∠AOD的平分线,且∠COB:∠AOD=4:9.
(1)写出图中∠BOD的余角和补角;
(2)求∠AOC的度数

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.研究数轴我们发现有许多重要的规律:
例如,若数轴上![]() 点、
点、![]() 点表示的数分别为
点表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点
的中点![]() 表示的数为
表示的数为![]() .
.
(问题情境)
在数轴上,点![]() 表示的数为-20,点
表示的数为-20,点![]() 表示的数为10,动点
表示的数为10,动点![]() 从点
从点![]() 出发沿数轴正方向运动,同时,动点
出发沿数轴正方向运动,同时,动点![]() 也从点
也从点![]() 出发沿数轴负方向运动,已知运动到4秒钟时,
出发沿数轴负方向运动,已知运动到4秒钟时,![]() 、
、![]() 两点相遇,且动点
两点相遇,且动点![]() 、
、![]() 运动的速度之比是
运动的速度之比是![]() (速度单位:单位长度/秒).
(速度单位:单位长度/秒).
![]()
![]()
备用图
(综合运用)
(1)点![]() 的运动速度为______单位长度/秒,点
的运动速度为______单位长度/秒,点![]() 的运动速度为______单位长度/秒;
的运动速度为______单位长度/秒;
(2)当![]() 时,求运动时间;
时,求运动时间;
(3)若点![]() 、
、![]() 在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点
在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点![]() 、
、![]() 的运动,线段
的运动,线段![]() 的中点
的中点![]() 也随着运动.问点
也随着运动.问点![]() 能否与原点重合?若能,求出从
能否与原点重合?若能,求出从![]() 、
、![]() 相遇起经过的运动时间,并直接写出点
相遇起经过的运动时间,并直接写出点![]() 的运动方向和运动速度;若不能,请说明理由.
的运动方向和运动速度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明.

供选择的三个条件(请从其中选择一个):
①AB=ED;
②BC=EF;
③∠ACB=∠DFE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com