
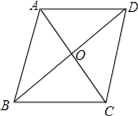
【题目】如图,在![]() ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8.
ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8.
(1)求证:四边形ABCD是菱形;
(2)过点A作AH⊥BC于点H,求AH的长.
【答案】(1)证明见解析(2) ![]()
【解析】试题分析:(1)由平行四边形的对角线互相平分得到△AOB的两条边OA、OB的长度,则根据勾股定理的逆定理判定∠AOB=90°,即平行四边形的对角线互相垂直平分,故四边形ABCD是菱形.
(2)根据菱形的不变性,用不同方法求面积:平行四边形的面积=菱形的面积,可求解.
试题解析:(1)证明:∵在![]() ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8,
ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8,
∴AO=![]() AC=3,BO=
AC=3,BO=![]() BD=4,
BD=4,
∵AB=5,且32+42=52,
∴AO2+BO2=AB2,
∴△AOB是直角三角形,且∠AOB=90°,
∴AC⊥BD,
∴四边形ABCD是菱形;
(2)解:如图所示:
∵四边形ABCD是菱形,
∴BC=AB=5,
∵S△ABC=![]() ACBO=
ACBO=![]() BCAH,
BCAH,
∴![]() ×6×4=
×6×4=![]() ×5×AH,
×5×AH,
解得:AH=![]() .
.



科目:初中数学 来源: 题型:
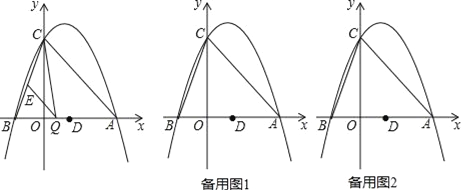
【题目】如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A坐标为(4,0).
(1)求该抛物线的解析式;
(2)抛物线的顶点为N,在x轴上找一点K,使CK+KN最小,并求出点K的坐标;
(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(4)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年淘宝网都会举办“双十一”购物狂欢节,许多商家都会利用这个契机进行打折让利的促销活动.甲网店销售一件A商品的成本为36元,网上标价为110元.“双十一”活动当天,为了吸引买主,连续两次降价销售A商品,问平均每次降价率为多少时,才能使这件A商品的利润率为10%?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市商店为了对某种商品促销,将定价为3元的商品,以下列方式优惠销售:若购买不超过5件,按原价付款;若一次性购买5件以上,超过部分打八折.如果用27元钱,最多可以购买该商品( )件
A. 9B. 10C. 11D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
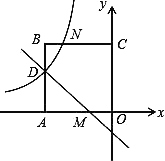
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y =![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(x1 , y1)是一次函数y=﹣x+b+1图象上一点,若x1<0,y1<0,则b的取值范围是( )
A.b<0
B.b>0
C.b>﹣1
D.b<﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知某小区的两幢10层住宅楼间的距离为AC="30" m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3 m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α .

(1) 用含α的式子表示h(不必指出α的取值范围);
(2) 当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光 ?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com