
【题目】如图,在![]() 中,点O是边AC上一个动点,过点O作直线
中,点O是边AC上一个动点,过点O作直线![]() //BC,分别交
//BC,分别交![]() ,外角
,外角![]() 的平分线于点E、F.
的平分线于点E、F.

(1)猜想与证明,试猜想线段OE与OF的数量关系,并说明理由.
(2)连接AE,AF,问:当点O在边AC上运动时到什么位置时,四边形AECF是矩形?并说明理由.
(3)若AC边上存在一点O,使四边形AECF是正方形,猜想![]() 的形状并证明你的结论.
的形状并证明你的结论.
【答案】(1)OE=OF,理由见解析.
(2)当点O在边AC上运动到AC中点时,四边形AECF是矩形;
理由见解析.
(3)△ABC是直角三角形;证明见解析.
【解析】
(1)根据CE平分∠ACB,MN∥BC,找到相等的角,即∠OEC=∠ECB,再根据等边对等角得OE=OC,同理OC=OF,可得EO=FO.
(2)利用矩形的判定解答,即有一个内角是直角的平行四边形是矩形.
(3)利用已知条件及正方形的性质问题可解.
(1)证明:∵CE是∠ACB的平分线,
∴∠ACE=∠BCE,
∵MN∥BC,
∴∠BCE=∠E,
∴∠ACE=∠E,
∴OE=OC,
同理可证OC=OF,
∴OE=OF;
(2)解:如图

当点O在边AC上运动到AC中点时,四边形AECF是矩形.
理由是:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵CE平分∠ACB,CF平分∠ACG,
∴∠ECF=![]() ∠ACB+
∠ACB+![]() ∠ACG=
∠ACG=![]() (∠ACB+∠ACG)=90°,
(∠ACB+∠ACG)=90°,
∴平行四边形AECF是矩形.
(3)△ABC是直角三角形
理由是:∵四边形AECF是正方形,
∴AC⊥EN,故∠AOM=90°,
∵MN∥BC,
∴∠BCA=∠AOM,
∴∠BCA=90°,
∴△ABC是直角三角形.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】根据要求,解答下列问题.
(1)解方程组:![]() .
.
(2)解下列方程组,只写出最后结果即可:①![]() ;②
;②![]() .
.
(3)以上每个方程组的解中,x值与y值有怎样的大小关系?
(4)观察以上每个方程组的外形特征,请你构造一个具有此特征的方程组,并用(3)中的结论快速求出其解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD对角线AC上一动点,EF⊥AC且交AD于E,交CD的延长线于点G,连接CE和AG.
(1)求证:△ADG≌△CDE;
(2)当CE平分∠ACD时,求tan∠AGD.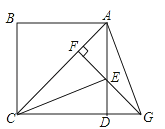
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小杨一家三人随旅游团去九寨沟旅游,小杨把旅途的费用支出情况制成了如图所示的统计图.
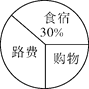
(1)哪一部分的费用占整个支出的![]() ?
?
(2)若他们共交给旅行社8600元,则在食宿上用去多少元?
(3)以上条件不变,这一家往返的路费共多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连结PM并延长到点E,使ME=PM,连结DE.
(1)请你利用图2,选择Rt△ABC内的任意一点P按上述方法操作;

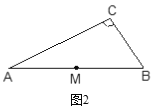
(2)经历(1)之后,观察两图形,猜想线段DE和线段BC之间有怎样的数量和位置关系?请选择其中的一个图形证明你的猜想;
(3)观察两图,你还可得出AC和DE相关的什么结论?请说明理由.
(4)若以A为坐标原点,建立平面直角坐标系,其中A、C、D的坐标分别为(0,0),(5,3),(4,2),能否在平面内找到一点M,使以A、C、D、M为点构造成平行四边形,若不能,说明理由,若能,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)经过多长时间,当PQ不平行于CD时,有PQ=CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知A(0,-2),B(-2,1),C(3,2)
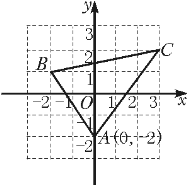
(1)求线段AB、BC、AC的长;
(2)把A、B、C三点的横坐标、纵坐标都乘以2,得到A′、B′、C′的坐标,求A′B′、B′C′、A′C′的长;
(3)以上六条线段成比例吗?
(4)△ABC与△A′B′C′的形状相同吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com