
【题目】如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( ) 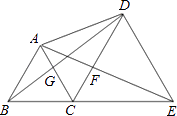
A.△ACE≌△BCD
B.△BGC≌△AFC
C.△DCG≌△ECF
D.△ADB≌△CEA
【答案】D
【解析】解:∵△ABC和△CDE都是等边三角形, ∴BC=AC,CE=CD,∠BCA=∠ECD=60°,
∴∠BCA+∠ACD=∠ECD+∠ACD,
即∠BCD=∠ACE,
∴在△BCD和△ACE中  ,
,
∴△BCD≌△ACE(SAS),
故A成立,
∴∠DBC=∠CAE,
∵∠BCA=∠ECD=60°,
∴∠ACD=60°,
在△BGC和△AFC中  ,
,
∴△BGC≌△AFC,
故B成立,
∵△BCD≌△ACE,
∴∠CDB=∠CEA,
在△DCG和△ECF中  ,
,
∴△DCG≌△ECF,
故C成立,
故选:D.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°.


科目:初中数学 来源: 题型:
【题目】已知O为直线AB上一点,∠COE为直角,OF平分∠AOE.
(1)如图1,若∠COF=30°,则∠BOE=_______;若∠COF=m°,则∠BOE=_______,∠BOE和∠COF的数量关系为___________;
(2)当射线OE绕点O逆时针旋转到图2的位置时,(1)中∠BOE和∠COF的数量关系是否仍成立?请说明理由.
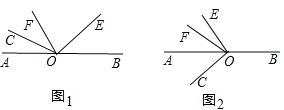
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年4月,我市开展了“北海历史文化进课堂”的活动,北海某校政教处就同学们对北海历史文化的了解程度进行随机抽样调查,并绘制成了如下两幅不完整的统计图. 
根据统计图中的信息,解答下列问题:
(1)本次调查的样本容量是多少,调查中“了解很少”的学生占多少;
(2)补全条形统计图;
(3)若全校共有学生900人,那么该校约有多少名学生“很了解”北海的历史文化?
(4)通过以上数据的分析,请你从爱家乡、爱北海的角度提出自己的观点和建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人先后从公园大门出发,沿绿道向码头步行,乙先到码头并在原地等甲到达.图1是他们行走的路程y(m)与甲出发的时间x(min)之间的函数图象.
(1)求线段AC对应的函数表达式;
(2)写出点B的坐标和它的实际意义;
(3)设d(m)表示甲、乙之间的距离,在图2中画出d与x之间的函数图象(标注必要数据).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是从一幅扑克牌中取出的两组牌,分别是黑桃1,2,3,4红桃1,2,3,4,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,那么摸出的两张牌面数字之和等于7的概率是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动:第1次点A向左移动3个单位长度至点A1,第2次从点A1向右移动6个单位长度至点A2,第3次从点A2向左移动9个单位长度至点A3,…,按照这种移动方式进行下去,点A2019表示的数,是______.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,小丽用尺规这样作图:(1),以点O为圆心,任意长为半径作弧,交OA,OB于D,E两点;(2)分别以点D,E为圆心,大于 ![]() DE的长为半径作弧,两弧交于点C;第三部,作射线OC并连接CD,CE,下列结论不正确的是( )
DE的长为半径作弧,两弧交于点C;第三部,作射线OC并连接CD,CE,下列结论不正确的是( ) 
A.∠1=∠2
B.S△OCE=S△OCD
C.OD=CD
D.OC垂直平分DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面的例题:
例题:已知二次三项式x2-4x+m有一个因式是x+3,求另一个因式以及m的值.
解:设另一个因式为x+n,则
x2-4x+m=(x+3)(x+n),
∴x2-4x+m=x2+(n+3)x+3n,
∴![]() ,解得
,解得![]() ,
,
∴另一个因式为x-7,m的值为-21.
问题:仿照以上方法解答下面的问题:
已知二次三项式2x2+3x-k有一个因式是2x-5,求另一个因式以及k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com