
【题目】如图,在以![]() 为直径的半
为直径的半![]() 上有
上有![]() C,点
C,点![]() 在
在![]() 上,过圆心
上,过圆心![]() 作
作![]() 的于点
的于点![]() 的延长线交于点
的延长线交于点![]() ,连结
,连结![]() ,若
,若![]() .
.
![]() 试说明
试说明![]() ;
;
![]() 若
若![]() 的面积为
的面积为![]() 面积的
面积的![]() 倍,连接
倍,连接![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值和
的值和![]() 的长:
的长:
![]() 在
在![]() 的条件下,延长
的条件下,延长![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,直接写
,直接写![]() 的长
的长
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连接BC由垂径定理可得OF垂直平分CD,得出△CDE是等腰直角三角形,∠DCE=∠CDE=45°,再根据圆的内接四边形的性质即可得出答案;
(2)连接OC、BD,得出 AE=3DE=![]() ,AD=
,AD=![]() ,由勾股定理计算出AC的长度,再由圆周角定理证出△ABC是等腰直角三角形,得出BC、AC和AB的长度,进而由勾股定理得出BD的长度,再利用圆周角定理即可得出tan∠ACD的值;证明△PCF∽△ABD,利用相似比即可得出OP的长度;
,由勾股定理计算出AC的长度,再由圆周角定理证出△ABC是等腰直角三角形,得出BC、AC和AB的长度,进而由勾股定理得出BD的长度,再利用圆周角定理即可得出tan∠ACD的值;证明△PCF∽△ABD,利用相似比即可得出OP的长度;
(3)由等腰直角三角形的性质得出OC⊥AB,证明△OCG∽△EAG,利用相似比即可得出答案.
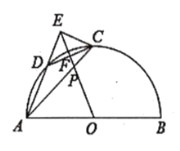
解:(1)证明:连接BC,如图1所示:
∵OF⊥CD
∴DF=CF
∴DE=EC
∵∠DEC=90°
∴△CDE是等腰直角三角形
∴∠DCE=∠CDE=45°
∴∠ABC=∠CDE=45°
∵AB是直径
∴∠ACB=90°
∴∠BAC=45°

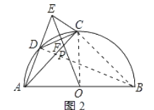
(2)连接OC、BD,如图2所示:
∵DF=CF=1
∴CD=2,△CDE是等腰直角三角形
∴ED=EC=![]()
∵△ACE的面积为△DCE面积的3倍
∴AE=3DE=![]() ,AD=
,AD=![]()
∴AC=![]()
∵AB是半圆的直径
∴∠ACB=∠ADB=90°
∵∠BAC=45°
∴△ABC是等腰直角三角形
∴BC=AC=![]() ,AB=
,AB=![]() AC=2
AC=2![]()
∴OC=OA=OB=![]() ,BD=
,BD=![]()
∵∠ACD=∠ABD
∴tan∠ACD= tan∠ABD=![]()
∵∠PFC=∠ADB=90°
∴△PCF∽△ABD
∴![]()
解得:PF=![]()
∵OF=![]()
∴OP=OF-PF=![]()
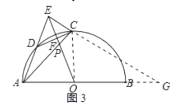
(3)如图3所示:
∵△ABC是等腰直角三角形,OA=OB
∴OC⊥AB
∴∠COG=∠DEC=90°
∵∠G=∠G
∴△OCG∽△EAG
∴![]()
即![]()
∴BG=![]() ,CG=
,CG=![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月,若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=![]() x-2与反比例函数y=
x-2与反比例函数y=![]() 的图象相交于点A(2, n) ,与x轴相交于点B.
的图象相交于点A(2, n) ,与x轴相交于点B.
(1)求k 的值以及点 B 的坐标;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)在y轴上是否存在点P,使PA+PB的值最小?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
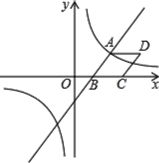
【题目】如图,已知反比例函数![]() 与一次函数
与一次函数![]() 的图象相交于点A、点D,且点A的横坐标为1,点D的纵坐标为-1,过点A作AB⊥x轴于点B,△AOB的面积为1.
的图象相交于点A、点D,且点A的横坐标为1,点D的纵坐标为-1,过点A作AB⊥x轴于点B,△AOB的面积为1.
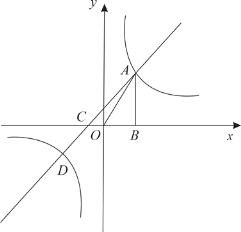
(1)求反比例函数和一次函数的解析式;
(2)若一次函数y=ax+b的图像与x轴交于点C,求∠ACO的度数.
(3)结合图像直接写出,当![]() 时,x的取值范围.
时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() 四张不透明的卡片,除正面上的图案不同外,其他均相同,将这四张卡片背 面向上洗匀后放在桌面上.
四张不透明的卡片,除正面上的图案不同外,其他均相同,将这四张卡片背 面向上洗匀后放在桌面上.
(1)从中随机取出一张卡片,卡片上的图案是中心对称图形的概率是_____;
(2)若从四张卡片中随机拿出两张卡片,请用画树状图或列表的方法,求抽取的两张卡片都是轴对称图形的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机抽取了该校部分学生的年龄作为样本,经过数据整理,绘制出如下不完整的统计图.依据相关信息解答以下问题:
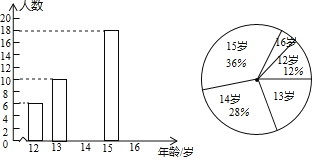
(1)写出样本容量 ,并补全条形统计图;
(2)写出样本的众数 岁,中位数 岁;
(3)若该校一共有600名学生.估计该校学生年龄在15岁及以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了创建书香校园,去年购买了一批图书.其中科普书的单价比文学书的单价多8元,用1800元购买的科普书的数量与用l000元购买的文学书的数量相同.
(1)求去年购买的文学书和科普书的单价各是多少元;
(2)这所学校今年计划再购买这两种文学书和科普书共200本,且购买文学书和科普书的总费用不超过2088元.今年文学书的单价比去年提高了20%,科普书的单价与去年相同,且每购买1本科普书就免费赠送1本文学书,求这所学校今年至少要购买多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的半径为5,点A的坐标为(3,0),
的半径为5,点A的坐标为(3,0),![]() 与x轴相交于点B,C,交y轴正半轴于点D.
与x轴相交于点B,C,交y轴正半轴于点D.
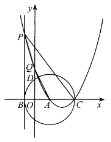
(1)求点B,D的坐标;
(2)过点B作![]() 的切线,与过点A,C的抛物线交于点P.抛物线交y轴正半轴于点Q.若P的纵坐标为t,四边形PQAC的面积为y.
的切线,与过点A,C的抛物线交于点P.抛物线交y轴正半轴于点Q.若P的纵坐标为t,四边形PQAC的面积为y.
①求y与t的函数关系式;
②若△PBO与△DOA相似,求![]() 取最小值时m的值.
取最小值时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年10月10日傍晚18:10左右,江苏省无锡市山区312国道上海方向K135处,锡港路上跨桥出现桥面侧翻,造成3人死亡,2人受伤,尽管该事故原因初步分析为半挂牵引车严重超载导致桥梁发生侧翻,但是也引起了社会各界对桥梁设计安全性的担忧,我市积极开展对桥梁结构设计的安全性进行评估(已知:抗倾覆系数越高,安全性越强;当抗倾覆系数≥2.5时,认为该结构安全),现在重庆市随机抽取了甲、乙两个设计院,对其各自在建的或已建的20座桥梁项目进行排查,将得到的抗倾覆数据进行整理、描述和分析(抗倾覆数据用x表示,共分成6组:A.0≤x<2.5,B.2.5≤x<5.0,C.5.0≤x<7.5,D.7.5≤x<10.0,E.10.0≤x<12.5,F.12.5≤x<15),下面给出了部分信息;
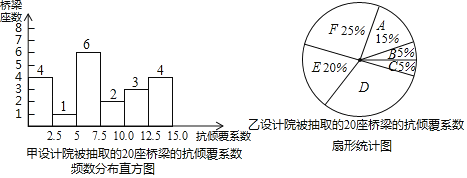
其中,甲设计院C组的抗倾覆系数是:7,7,7,6,7,7;
乙设计院D组的抗倾覆系数是:8,8,9,8,8,8;
甲、乙设计院分别被抽取的20座桥梁的抗倾覆系数统计表
设计院 | 甲 | 乙 |
平均数 | 7.7 | 8.9 |
众数 | a | 8 |
中位数 | 7 | b |
方差 | 19.7 | 18.3 |
根据以上信息解答下列问题:
(1)扇形统计图中D组数据所对应的圆心角是 度,a= ,b= ;
(2)根据以上数据,甲、乙两个设计院中哪个设计院的桥梁安全性更高,说明理由(一条即可): ;
(3)据统计,2018年至2019年,甲设计院完成设计80座桥梁,乙设计院完成设计120座桥梁,请估算2018年至2019年两设计院的不安全桥梁的总数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com