
分析 分四种情况,点C分别在四个象限内,画出图形,根据等边三角形的性质得出顶点C的坐标.
解答 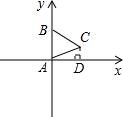 解:当点C在第一象限时,过点C作CD⊥x轴,
解:当点C在第一象限时,过点C作CD⊥x轴,
∵△ABC是等边三角形,AB=1,
∴AB=AC=1,∠CAD=30°,
∴CD=,AD=$\frac{1}{2}$$\sqrt{3}$,
∴C($\frac{1}{2}$$\sqrt{3}$,$\frac{1}{2}$);
当点C在第二象限时,点C坐标与($\frac{1}{2}$$\sqrt{3}$,$\frac{1}{2}$)关于y轴对称,从而得出第二个点C坐标(-$\frac{1}{2}$$\sqrt{3}$,$\frac{1}{2}$);
从而得出另外两个点C坐标(-$\frac{1}{2}$$\sqrt{3}$,-$\frac{1}{2}$);($\frac{1}{2}$$\sqrt{3}$,-$\frac{1}{2}$),
所以第三个顶点C的坐标为($\frac{1}{2}$$\sqrt{3}$,$\frac{1}{2}$);(-$\frac{1}{2}$$\sqrt{3}$,-$\frac{1}{2}$);($\frac{1}{2}$$\sqrt{3}$,-$\frac{1}{2}$),(-$\frac{1}{2}$$\sqrt{3}$,$\frac{1}{2}$).
点评 本题考查的是等边三角形的性质,根据题意画出图形,利用数形结合求解是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{3\sqrt{3}}{5}$ | D. | $\frac{15\sqrt{3}}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com