练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

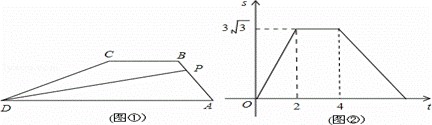
    如图①，在梯形ABCD中，AD∥BC，∠A=60°，动点P从A点出发，以1cm/s的速度沿着A→B→C→D的方向不停移动，直到点P到达点D后才停止．已知△PAD的面积S（单位：cm2）与点P移动的时间（单位：s）的函数如图②所示，则下列结论：①AB＝BC＝2cm；②cos∠CDA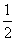＝；③梯形ABCD的面积为 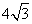cm2；④点P从开始移动到停止移动一共用了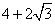（）秒；其中正确的结论是(      )。

                             （第10题）

    A．①②      B．①③      C．①③④      D．①②③④


    C


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


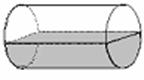
    如右图一只封闭的圆柱形水桶（桶的厚度忽略不计），底面直径为20cm，母线长为40cm，盛了半桶水，现将该水桶水平放置后如图所示，则水所形成的几何体的表面积为（      ）

    A．800 cm2                       B． (800+400π) cm2                         

    C．(800+500π)cm2                D．(1600+1200π)cm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若实数a、b满足a+b=5，a2b+ab2=-10，则ab的值是（     ）

    A.-2             B.2            C.-50         D.50

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    为迎接中国森博会，某商家计划从厂家采购A，B两种产品共20件，产品的采购单价（元/件）是采购数量（件）的一次函数．下表提供了部分采购数据．

    （1）设A产品的采购数量为x（件），采购单价为y1（元/件），求y1与x的关系式；

    （2）经商家与厂家协商，采购A产品的数量不少于B产品数量的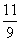，且A产品采购单价不低于1200元．求该商家共有几种进货方案；

    （3）该商家分别以1760元/件和1700元/件的销售单价售出A，B两种产品，且全部售完．在（2）的条件下，求采购A种产品多少件时总利润最大，并求最大利润．

    采购数量（件）

    1

    2

    …

    A产品单价（元/件）

    1480

    1460

    …

    B产品单价（元/件）

    1290

    1280

    …

    查看答案和解析>>

    科目：初中数学 来源： 题型：


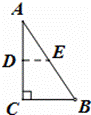
    如图，直角三角形纸片ABC的∠C为90°，将三角形纸片沿着图示的中位线DE剪开，然后把剪开的两部分重新拼接成不重叠的图形，下列选项中不能拼出的图形是（　 　）

    A．直角梯形      B．矩形        C．等腰梯形     D．平行四边形 

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    平面内有四个不同的点A、O、B、C，其中∠AOB=120°，∠ACB=60°，AO=BO=2，则满足题意的OC长度的取值范围是         。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知梯形ABCD,   AD∥BC，AB⊥BC，AD=1，AB=2，BC=3，问题：

    （1）如图1，P为AB边上一点，以PD、PC为边做平行四边形PCQD，请问对角线PQ，DC的长能否相等，为什么？

    （2）如图2，P为AB边上任意一点，以PD、PC为边做平行四边形PCQD，请问对角线PQ的长是否存在最小值？若果存在，请求出最小值；如果不存在，请说明理由。

    （3）P为AB边上任意一点，延长PD到E，使DE=PD，以PE、PC为边做平行四边形PCQE，请探究对角线PQ的长是否也存在最小值？若果存在，请求出最小值；如果不存在，请说明理由。

     

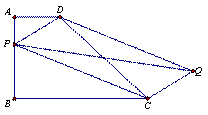
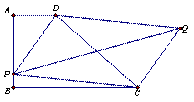
    （图1）                              （图2）                              

    查看答案和解析>>

    科目：初中数学 来源： 题型：


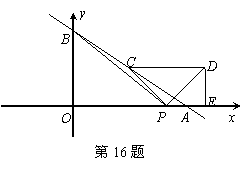
     如图：直线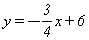与x，y轴分别交于A，B，C是AB的中点，点P从A出发以每秒1个单位的速度沿射线AO方向运动，将点C绕P顺时针旋转90°得到点D，作DE⊥x轴，垂足为E，连接PC，PD，PB.设点P的运动时间为t秒（0≤t≤16）,当以P，D，E为顶点的三角形与△BOP相似时，写出所有t的值：      

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分解因式：=_________________                 

    查看答案和解析>>

    同步练习册答案