
·ÖĪö £Ø1£©øł¾ŻĢāŅāæɵƷ½³Ģx+$\frac{1}{x}$=m+$\frac{1}{m}$µÄ½āĪŖx1=m£¬x2=$\frac{1}{m}$£¬“śČė¼ģŃ鼓æÉµĆ£»
£Ø2£©¢Łøł¾Ży3+$\frac{1}{y^3}$=8+$\frac{1}{8}$æɵĆy3=8£¬$\frac{1}{{y}^{3}}$=$\frac{1}{8}$£¬æɵƓš°ø£»
¢ŚĮī4x-8=t£¬Ōņx=$\frac{t+8}{4}$£¬Ō·½³Ģ±äŠĪĪŖ$\frac{t}{4}$+2+$\frac{1}{t}$=$\frac{{{a^2}+4a+1}}{2a}$£¬¼“$\frac{t}{2}$+$\frac{2}{t}$=a+$\frac{1}{a}$£¬µĆ³ö$\frac{t}{2}$=a£¬¼“t=2a£¬µĆ³ö2x-4=2a£¬½āÖ®æÉµĆ£®
½ā“š ½ā£ŗ£Ø1£©¹ŲÓŚx·½³Ģx+$\frac{1}{x}$=m+$\frac{1}{m}$µÄ½āĪŖx1=m£¬x2=$\frac{1}{m}$£¬
ŃéÖ¤£ŗµ±x=mŹ±£¬×ó±ß=m+$\frac{1}{m}$=ÓŅ±ß£¬”ąx=mŹĒøĆ·ÖŹ½·½³ĢµÄ½ā£»
µ±x=$\frac{1}{m}$Ź±£¬×ó±ß=$\frac{1}{m}$+$\frac{1}{\frac{1}{m}}$=$\frac{1}{m}$+m=ÓŅ±ß£¬”ąx=$\frac{1}{m}$ŹĒøĆ·ÖŹ½·½³ĢµÄ½ā£»
£Ø2£©¢Ł”ßy3+$\frac{1}{y^3}$=8+$\frac{1}{8}$£¬
”ąy3=8£¬$\frac{1}{{y}^{3}}$=$\frac{1}{8}$£¬
”ąy=2£»
¢ŚĮī4x-8=t£¬Ōņx=$\frac{t+8}{4}$£¬
”ąŌ·½³Ģ±äŠĪĪŖ$\frac{t}{4}$+2+$\frac{1}{t}$=$\frac{{{a^2}+4a+1}}{2a}$£¬
$\frac{t}{4}$+$\frac{1}{t}$=$\frac{{a}^{2}+1}{2a}$£¬
$\frac{t}{2}$+$\frac{2}{t}$=$\frac{{a}^{2}+1}{a}$£¬¼“$\frac{t}{2}$+$\frac{2}{t}$=a+$\frac{1}{a}$£¬
Ōņ$\frac{t}{2}$=a£¬»ņ$\frac{2}{t}$=$\frac{1}{a}$£¬
”ąt=2a£¬
¼“4x-8=2a£¬
½āµĆ£ŗx=$\frac{2a+8}{4}$=$\frac{a+4}{2}$£®
µćĘĄ ±¾ĢāÖ÷ŅŖæ¼²é½ā·ÖŹ½·½³Ģ£¬ŹģĮ·ÕĘĪÕ»»ŌŖ·Ø½ā·ÖŹ½·½³ĢŹ½½āĢāµÄ¹Ų¼ü£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
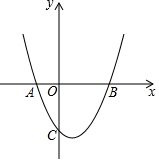 ČēĶ¼£¬Å×ĪļĻßy=x2-2x-3ÓėxÖį½»ÓŚA”¢BĮ½µć£¬ÓėyÖį½»ÓŚµćC£®
ČēĶ¼£¬Å×ĪļĻßy=x2-2x-3ÓėxÖį½»ÓŚA”¢BĮ½µć£¬ÓėyÖį½»ÓŚµćC£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
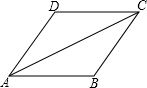 ČēĶ¼£¬ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬ACĘ½·Ö”ĻDAB£¬AB=4£¬ŌņĘ½ŠŠĖıߊĪABCDµÄÖܳ¤ĪŖ16£®
ČēĶ¼£¬ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬ACĘ½·Ö”ĻDAB£¬AB=4£¬ŌņĘ½ŠŠĖıߊĪABCDµÄÖܳ¤ĪŖ16£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
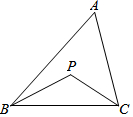 ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬BP”¢CP·Ö±šŹĒ”ĻABCŗĶ”ĻACBµÄ½ĒĘ½·ÖĻߣ®
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬BP”¢CP·Ö±šŹĒ”ĻABCŗĶ”ĻACBµÄ½ĒĘ½·ÖĻߣ®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com