
 如图,正方形A、B、C的边长分别为直角三角形的三边长,若正方形A、B的边长分别为3和5,则正方形C的面积为16.
如图,正方形A、B、C的边长分别为直角三角形的三边长,若正方形A、B的边长分别为3和5,则正方形C的面积为16. 科目:初中数学 来源: 题型:解答题
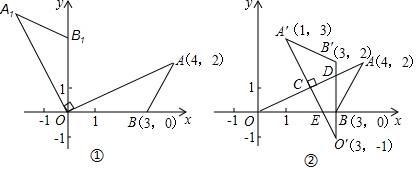
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知两个完全相同的直角三角形纸片△ABC、△DEF,如图放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,现将图中的△ABC绕点F按每秒10°的速度沿逆时针方向旋转180°,在旋转的过程中,△ABC恰有一边与DE平行的时间为3或12或15s.
已知两个完全相同的直角三角形纸片△ABC、△DEF,如图放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,现将图中的△ABC绕点F按每秒10°的速度沿逆时针方向旋转180°,在旋转的过程中,△ABC恰有一边与DE平行的时间为3或12或15s.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{a}^{3}}{{b}^{2}}$ | B. | a3-b2 | C. | a3b2 | D. | 3a-2b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1:4 | B. | 1:2 | C. | 2:1 | D. | 1:$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
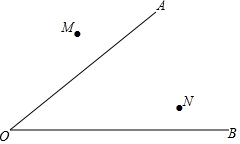 2016年6月10日,我海军两艘军舰“温州526舰”、“马鞍山525舰”在我钓鱼岛海域进行巡航.如图,两舰约定在点P会合,已知P点到M、N两地的距离相等,且到OA、OB两条航线的距离相等,请在下图中找出P点的位置.(保留作图痕迹,不写作法)
2016年6月10日,我海军两艘军舰“温州526舰”、“马鞍山525舰”在我钓鱼岛海域进行巡航.如图,两舰约定在点P会合,已知P点到M、N两地的距离相等,且到OA、OB两条航线的距离相等,请在下图中找出P点的位置.(保留作图痕迹,不写作法)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com