
【题目】如图![]() ,二次函数
,二次函数![]() (
(![]() 、
、![]() 为参数,其中
为参数,其中![]() )的图象与
)的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
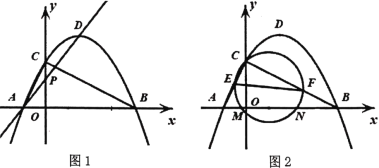
(1)若![]() ,求
,求![]() 的值(结果用含
的值(结果用含![]() 的式子表示);
的式子表示);
(2)若![]() 是等腰三角形,直线
是等腰三角形,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() .求抛物线的解析式;
.求抛物线的解析式;
(3)如图![]() ,已知
,已知![]() ,
,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,且
上的动点,且![]() ,若以
,若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,并交
,并交![]() 轴于
轴于![]() 、
、![]() 两点,求
两点,求![]() 的最大值.
的最大值.
【答案】(1)tan∠CBA=-2a;(2)![]() ;(3)MN的最大值=
;(3)MN的最大值=![]()
【解析】
(1)将![]() 代入函数解析式,求得B点坐标,在直角三角形BOC中,利用正切定义直接求得
代入函数解析式,求得B点坐标,在直角三角形BOC中,利用正切定义直接求得![]() ;
;
(2)利用对称轴可知D的横坐标,过D做DH⊥x轴,交x轴于点H,因为OP∥DH,利用平行线分线段成比例,求得A、B两点坐标,代入解析式可得到![]() ,再对
,再对![]() 分情况讨论即可;
分情况讨论即可;
(3)利用圆周角定理可知![]() 解得a,求得C点,同时由已知EF=3,可知取EF的中点Q,过Q做QH⊥X轴于点H,则Q在以C为圆心,
解得a,求得C点,同时由已知EF=3,可知取EF的中点Q,过Q做QH⊥X轴于点H,则Q在以C为圆心,![]() 为半径的圆上运动,在Rt△QHN中,
为半径的圆上运动,在Rt△QHN中,![]() ,求HN的最大值等价求QH的最小值,求得QH推得HN,进而得到MN.
,求HN的最大值等价求QH的最小值,求得QH推得HN,进而得到MN.
(1)∵![]()
∴![]()
∴A(-2,0),B(5,0),C(-10a,0)
∴tan∠CBA=![]()
(2)由已知![]()
过D做DH⊥X轴,交X轴于点H
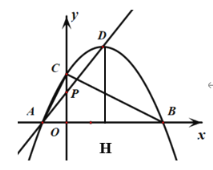
∵OP∥DH,AP:DP=2:3,![]()
∴![]()
∴OA=1,A(-1,0),B(4,0)
∴![]()
∴![]()
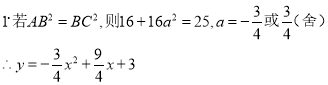
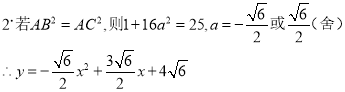
![]()
(3)∵A(-1,0),B(4,0)![]() 且以EF为直径的圆经过点C
且以EF为直径的圆经过点C
∴![]() ,解得
,解得![]()
∴C(0.2)
∵![]()
取EF的中点Q,过Q做QH⊥x轴于点H,则Q在以C为圆心,![]() 为半径的圆上运动
为半径的圆上运动
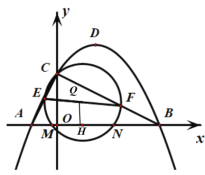
∵MN=2HN
在Rt△QHN中,![]() ,求HN的最大值等价求QH的最小值
,求HN的最大值等价求QH的最小值
∵QH的最小值=![]()
∴HN的最大值=
∴MN的最大值=![]()


科目:初中数学 来源: 题型:
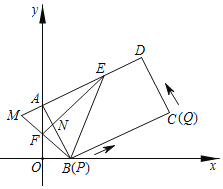
【题目】如图,在直角坐标系中,长方形ABCD(每个内角都是90°)的顶点的坐标分别是A(0,m),B(n,0),(m>n>0),点E在AD上,AE=AB,点F在y轴上,OF=OB,BF的延长线与DA的延长线交于点M,EF与AB交于点N.
(1)试求点E的坐标(用含m,n的式子表示);
(2)求证:AM=AN;
(3)若AB=CD=12cm,BC=20cm,动点P从B出发,以2cm/s的速度沿BC向C运动的同时,动点Q从C出发,以vcm/s的速度沿CD向D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
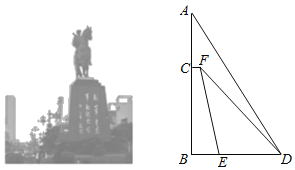
【题目】2018年9月21日“盐城大铜马“顺利回归,如图,小丽和小明决定用所学的知识测量大铜马AB的高度,按照以下方式合作并记录所得数据:小明测得基座下部BE长为1.8米,基座BC高为6.12米,在E点处测得点F的仰角为80.72°,小丽沿直线BE步行到达点D处测得点A和点F的仰角分别为60.18°和50.75°,若A、B、C、D、E、F在同一平面内且B、E、D和A、C、B分别在同一直线上,请分别求出CF和大铜马AB的高度.(结果精确到0.01米,参考数据sin80.72°=0.987,cos80.72°=0.161,tan80.72°=6.12,sin60.18°=0.868,cos60.18°=0.497,tan60.18°=1.74,sin50.75°=0.774,cos50.75°=0.663,tan50.75°=1.224)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A市准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的提示牌和垃圾箱,若购买2个提示牌和3个垃圾箱共需550元,且垃圾箱的单价是提示牌单价的3倍.
(1)求提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地提高业主垃圾分类的意识,某小区物业管理委员会决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买3个温馨提示牌和2个垃圾箱共需要420元,且每个温馨提示牌比垃圾箱便宜60元.
(1)问购买1个温馨提示牌和1个垃圾箱各需要多少元?
(2)如果需要购买温馨提示牌和垃圾箱共80个,且费用不超过8000元,问最多可以购买垃圾箱多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分,某高校组织课外小组在我市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如下不完整统计表和统计图(如图).已知![]() ,
,![]() 两组户数频数宜方图的高度比为1:5.
两组户数频数宜方图的高度比为1:5.
月信息消费额分组统计表
组别 | 消费额/元 |
|
|
|
|
|
|
|
|
|
|
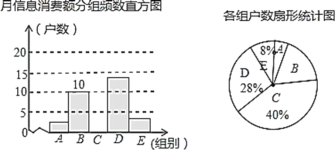
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有_________户;
(2请你补全频数直方图;
(3)以各组组中值代表本组的月信息消费额的平均数,计算课外小组抽取家庭的月信息消费额的平均数;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药,12周后,记录了两组患者的生理指标![]() 和
和![]() 的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者;
的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者;
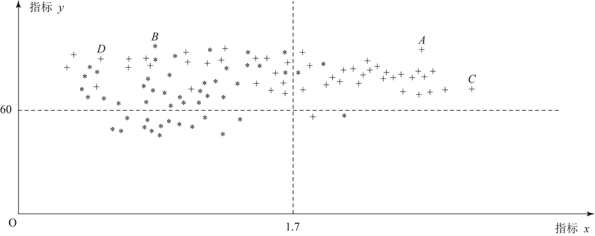
同时记录了服药患者在4周、8周、12周后的指标z的改善情况,并绘制成条形统计图.

根据以上信息,回答下列问题:
(1)从服药的50名患者中随机选出一人,求此人指标![]() 的值大于1.7的概率;
的值大于1.7的概率;
(2)设这100名患者中服药者指标![]() 数据的方差为
数据的方差为![]() ,未服药者指标
,未服药者指标![]() 数据的方差为
数据的方差为![]() ,则
,则![]()
![]() ;(填“>”、“=”或“<” )
;(填“>”、“=”或“<” )
(3)对于指标z的改善情况,下列推断合理的是 .
①服药4周后,超过一半的患者指标z没有改善,说明此药对指标z没有太大作用;
②在服药的12周内,随着服药时间的增长,对指标z的改善效果越来越明显.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com