
���� ��1������n=5��ֱ�ӵó����ۣ�
��2����ֱ��y=2x-1����ȡ����A��0��-1����B��0.5��0�������ݹ���x��ԳƵĵ�������ص�ó��������x��ԳƵĵ�����꣬���ô���ϵ�������ֱ�ߵĽ���ʽ���ɣ�
��3����ֱ��y=2x-1����ȡ����A��0��-1����B��0.5��0�����ó���ԭ��˳ʱ����ת90���Ķ�Ӧ��DE�����꣬���ô���ϵ�������ֱ�ߵĽ���ʽ���ɣ�
��� �⣺��1����n=5��
��ƽ�ƺ�����ֱ������Ӧ��������ʽΪ��y=2x+5��
�ʴ�Ϊ��y=2x+5��
��2����ֱ��y=2x-1����ȡ����A��0��-1����B��0.5��0���������x��ԳƵĵ������ΪA�䣨0��1����B�䣨0.5��0����
��ֱ��A��B��Ľ���ʽΪy=kx+b��k��0������$\left\{\begin{array}{l}{0.5k+b=0}\\{b=1}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-2}\\{b=1}\end{array}\right.$��
��ֱ��A��B��Ľ���ʽΪ��y=-2x+1��
��3����ֱ��y=2x-1����ȡ����A��0��-1����B��0.5��0��������ԭ��˳ʱ����ת90����Ӧ�������ΪD��-1��0����B�䣨0��-0.5����
��ֱ��DE�Ľ���ʽΪy=px+q����$\left\{\begin{array}{l}{-p+q=0}\\{q=-0.5}\end{array}\right.$�����$\left\{\begin{array}{l}{p=-0.5}\\{q=-0.5}\end{array}\right.$��
��ֱ��DE�Ľ���ʽΪ��y=-$\frac{1}{2}$x-$\frac{1}{2}$��
�ʴ�Ϊ��y=-$\frac{1}{2}$x-$\frac{1}{2}$��
���� ���⿼�����һ�κ�����ͼ���뼸�α任����֪���ô���ϵ������һ�κ�������ʽ�ķ����ǽ�����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�����ʡ֦���о��꼶3�µ��п�����ѧ�Ծ��������棩 ���ͣ���ѡ��
����ʽ��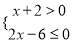 �Ľ⼯�������ϱ�ʾ��ȷ���ǣ� ��
�Ľ⼯�������ϱ�ʾ��ȷ���ǣ� ��
A. 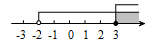 B.
B. 
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��1����һ�������ǵ�ֽ�壬����������Ƕ�Ϊ60�㣬�����۽Ƕ�Ϊ120�㣬ÿ���߶���ȣ��ֽ���ֽ�尴ͼ��2���и����϶���ص���ƴ�ɾ���ABCD����������ֽ������Ϊ9$\sqrt{3}$cm2�������ABCD���ܳ�Ϊ��������
��ͼ��1����һ�������ǵ�ֽ�壬����������Ƕ�Ϊ60�㣬�����۽Ƕ�Ϊ120�㣬ÿ���߶���ȣ��ֽ���ֽ�尴ͼ��2���и����϶���ص���ƴ�ɾ���ABCD����������ֽ������Ϊ9$\sqrt{3}$cm2�������ABCD���ܳ�Ϊ��������| A�� | 18cm | B�� | 8$\sqrt{3}$cm | C�� | ��2$\sqrt{3}$+6��cm | D�� | ��6$\sqrt{3}$+6��cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��O��ֱ��AB��һ�㣬��AOC=50�㣬���BOC�Ķ����ǣ�������
��ͼ��O��ֱ��AB��һ�㣬��AOC=50�㣬���BOC�Ķ����ǣ�������| A�� | 120�� | B�� | 130�� | C�� | 140�� | D�� | 150�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
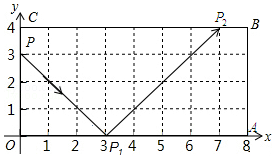 ��ͼ������С��ӵ�P��0��3������������ʾ�����˶���ÿ��С����������OABC�ı�ʱ����������ʱ����ǵ�������ǣ���С���1���������εı�ʱ����Ϊ��P1����2���������εı�ʱ����Ϊ��P2������n���������εı�ʱ����Ϊ��Pn�����P3�������ǣ�8��3������P2017�������ǣ�3��0����
��ͼ������С��ӵ�P��0��3������������ʾ�����˶���ÿ��С����������OABC�ı�ʱ����������ʱ����ǵ�������ǣ���С���1���������εı�ʱ����Ϊ��P1����2���������εı�ʱ����Ϊ��P2������n���������εı�ʱ����Ϊ��Pn�����P3�������ǣ�8��3������P2017�������ǣ�3��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com