
【题目】在![]() 中,
中,![]() 的平分线
的平分线![]() 与外角
与外角![]() 的平分线
的平分线![]() 所在的直线交于点
所在的直线交于点![]() .
.
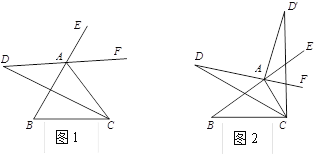
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,把![]() 沿
沿![]() 翻折,点
翻折,点![]() 落在
落在![]() 处.
处.
①当![]() 时,求
时,求![]() 的度数;②试确定
的度数;②试确定![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
科目:初中数学 来源: 题型:
【题目】解不等式、不等式组
(1)解不等式:![]() 并把它的解集表示在数轴上.
并把它的解集表示在数轴上.
(2)解不等式组: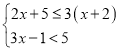 ,并求出这个不等式组的所有整数解.(要求利用数轴解不等式组)
,并求出这个不等式组的所有整数解.(要求利用数轴解不等式组)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别,某校模仿二维码建立了一个七年级学生身份识别系统,图2是七年级某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20+1.如图2第一行数字从左到右依次为0,1,0,1,序号为0×23+1×22+0×21+1×20+1=6表示该生为6班学生.则该系统最多能识别七年级的班级数是___个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建生态文明建设城市,对公路旁的绿化带进行全面改造.现有甲、乙两个工程队,甲队单独完成这项工程,刚好如期完成,每施工一天,需付工程款1.5万元;乙工程队单独完成这项工程要比规定工期多用a天,乙工程队每施工一天需付工程款1万元.若先由甲、乙两队一起合作b天,剩下的工程由乙队单独做,也正好如期完工
(1)当a=6,b=4时,求工程预定工期的天数.
(2)若a﹣b=2.a是偶数
①求甲队、乙队单独完成工期的天数(用含a的代数式表示)
②工程领导小组有三种施工方案:
方案一:甲队单独完成这项工程;
方案二:乙队单独完成这项工程;
方案三:先由甲、乙两队一起合作b天,剩下的工程由乙队单独做.
为了节省工程款,同时又能如期完工,请你选择一种方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 与
与![]() 不平行,
不平行,![]() .
.![]() 为四边形
为四边形![]() 的对角线,
的对角线,![]()
![]() 分别是
分别是![]() 的中点下列结论:①
的中点下列结论:①![]() ;②四边形
;②四边形![]() 是矩形;③
是矩形;③![]() 平分
平分![]() ④
④![]() ;⑤四边形
;⑤四边形![]() 是菱形.其中正确的个数是 ( )
是菱形.其中正确的个数是 ( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B与∠C的角平分线相交于点I,过点I作BC的平行线,分别交AB、AC于点D、E.若AB=9,AC=6,BC=8,则△ADE的周长是( )
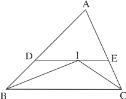
A. 14B. 15C. 17D. 23
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是△ABC的中线.

(1)利用尺规按下列要求作图,并在图中标明相应字母.(保留作图痕迹,不写作法)
①作线段AC的垂直平分线,分别交AC、AD、AB于点E、M、F;②连接CM、BM;
(2)若∠CAD=20°,求∠MCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0;④当y>0时,x的取值范围是﹣1≤x<3;
⑤当x<0时,y随x增大而增大.
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中的箭头所示方向运动,第一次从原点运动到点(2,2)第2次运动到点A(4,0),第3次接着运动到点(6,1)……按这样的运动规律,经过第2018次运动后动点P的坐标是____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com