
【题目】成都一机械厂接到生产一批机器设备的订单,要求必须在12天(含12天)内完成.已知每台机械设备的成本价为800元,该厂平时每天能生产该设备20台。为了加快进度,该厂采取工人分批日夜加班的方式,每天的生产量得到了提高。这样,第一天生产了22台,以后每天生产的设备都比前一天多2台。但由于机器损耗等原因,当每天生产的设备达到30台后,每多生产1台机械设备,当天生产的所有生产的设备每台的成本就增加20元。设生产这批设备的时间为x天,每天生产的机械设备为y台。
(1)直接写出y与x之间的函数关系式,并写出自变量x的取值范围。
(2)若这批机器设备的订购价格为每台1200元,该机械厂决定把获得最高利润的那一天的全部利润用来补贴困难职工。设该厂每天的利润为W元,试求出W与x之间的函数关系式,并求出该机械厂用来补贴给困难职工多少钱?
【答案】(1)y=2x+20(1≤x≤12);(2)12000元.
【解析】
试题解析:(1)根据该车间平时每天能生产设备20台,第一天生产了22台,以后每天生产的设备都比前一天多2台,直接得出生产这批设备的时间为x天,与每天生产的设备为y台之间的函数关系式;
(2)根据基本等量关系是:利润=(每台设备购价-每台设备成本价-增加的其他费用)×生产量即可得出答案.
试题解析:(1)∵该车间平时每天能生产设备20台,第一天生产了22台,以后每天生产的设备都比前一天多2台,
∴由题意可得出,生产这批设备的时间为x天,每天生产的设备为y台之间的函数关系式为:y=2x+20(1≤x≤12);
(2)当1≤x≤5时,W=(1200-800)×(2x+20)=800x+8000,
此时W随着x的增大而增大,
∴当x=5时,W最大值=12000;
当5<x≤12时,
W=[1200-800-20×(2x+20-30)]×(2x+20)
=-80(x-2.5)2+12500,
此时函数图象开口向下,在对称右侧,W随着x的增大而减小,又天数x为整数,
∴当x=6时,W最大值=11520元.
∵12000>11520,
∴当x=5时,W最大,且W最大值=12000元.
综上所述:
W=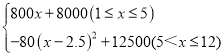 .
.
∴该车间捐献给困难职工12000元.


科目:初中数学 来源: 题型:
【题目】以下3个说法中:①在同一直线上的4点A、B、C、D只能表示5条不同的线段;②经过两点有一条直线,并且只有一条直线;③同一个锐角的补角一定大于它的余角.说法都正确的结论是( ).
A.②③ B.③ C.①② D.①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市规定,如果购买不超过50元的商品时,按全额收费;购买超过50元的商品时,超过部分按九折收费.某顾客在一次消费中,向售货员交纳了212元,那么在此次消费中该顾客购买了价值 元的商品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列命题中,该命题的逆命题成立的是( )
A. 线段垂直平分线上的点到这条线段两个端点的距离相等
B. 等边三角形是锐角三角形
C. 如果两个角是直角,那么它们相等
D. 如果两个实数相等,那么它们的平方相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com