

分析 (1)理由等腰三角形的三线合一的知识即可解决问题;
(2)将△AND绕点D顺时针旋转90?,得到△AFB,只要证明△AFM≌△ANM,△FBM是直角三角形即可;
(3)结论:BM2+DN2=MN2.只要证明∠MAN=45°,利用(2)的方法即可证明;
解答 解:(1)如图1中,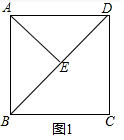
∵BD是正方形ABCD的对角线,
∴∠ABD=∠ADB=45?,
∵AE⊥BD,
∴∠ABE=∠BAE=45?;
(2)将△AND绕点D顺时针旋转90?,得到△AFB,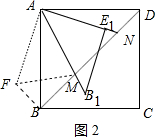
∴∠ADB=∠FBA,∠BAF=∠DAN,DN=BF,AF=AN,
∵在正方形ABCD中,AE⊥BD,
∴∠ADB=∠ABD=45?,
∴∠FBM=∠FBA+∠ABD=∠ADB+∠ABD=90?,
在Rt△BFM中,根据勾股定理得,FB2+BM2=FM2,
∵旋转△ABE得到△AB1E1,
∴∠E1AB1=45?,
∴∠BAB1+∠DAN=90?-45?=45?,
∵∠BAF=DAN,
∴∠BAB1+∠BAF=45?,
∴∠FAM=45?,
∴∠FAM=∠E1AB1,
∵AM=AM,AF=AN,
∴△AFM≌△ANM,
∴FM=MN,
∵BM2+FB2=FM2,
∴BM2+DN2=MN2.
(3)结论:BM2+DN2=MN2.
理由:如图3中,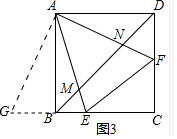
将△ADF绕点A顺时针旋转90?得到△ABG,
∴DF=GB,
∵正方形ABCD的周长为4AB,
△CEF周长为EF+EC+CF,
∵△CEF周长是正方形ABCD周长的一半,
∴4AB=2(EF+EC+CF),
∴2AB=EF+EC+CF
∵EC=AB-BE,CF=AB-DF,
∴2AB=EF+AB-BE+AB-DF,
∴EF=DF+BE,
∵DF=GB,
∴EF=GB+BE=GE,
由旋转得到AF=AG,
∵AE=AE,
∴△AEG≌△AEF,
∴∠EAG=∠EAF=45°,
同理可得BM2+DN2=MN2.
点评 本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,属于中考压轴题.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
| A. | 20.12×102 | B. | 0.2012×104 | C. | 2.012×103 | D. | 2.012×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.5615×106 | B. | 5.615×105 | C. | 56.15×104 | D. | 561.5×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
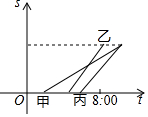 甲、乙、丙三车从A城出发匀速前往B城.在整个行程中,汽车离开A城的距离s与时刻t的对应关系如图所示.那么8:00时,距A城最远的汽车是( )
甲、乙、丙三车从A城出发匀速前往B城.在整个行程中,汽车离开A城的距离s与时刻t的对应关系如图所示.那么8:00时,距A城最远的汽车是( )| A. | 甲车 | B. | 乙车 | C. | 丙车 | D. | 甲车和乙车 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
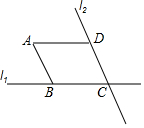 如图,直线l1与直线l2相交于点C,点B,D分别在l1,l2上,且BC=CD=3,分别过点B,D作l2,l1的平行线相交于点A.若点A到直线l1的距离为2,则点A到直线l2的距离为2.
如图,直线l1与直线l2相交于点C,点B,D分别在l1,l2上,且BC=CD=3,分别过点B,D作l2,l1的平行线相交于点A.若点A到直线l1的距离为2,则点A到直线l2的距离为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com