
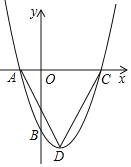
【题目】如图,抛物线y=x2+bx+c与x轴交于A,C两点,与y轴交于B点,抛物线的顶点为点D,已知点A的坐标为(﹣1,0),点B的坐标为(0,﹣3).
(1)求抛物线的解析式及顶点D的坐标.
(2)求△ACD的面积.
科目:初中数学 来源: 题型:
【题目】![]() 与
与![]() 都是等腰直角三角形,且
都是等腰直角三角形,且![]() ,
,![]() ,连接DC,点M、P、N分别为DE、DC、BC的中点
,连接DC,点M、P、N分别为DE、DC、BC的中点
(1)如图1,当点D、E分别在边AB、AC上,线段PM与PN的数量关系是______,位置关系是______;
(2)把等腰![]() 绕点A旋转到如图2的位置,连接MN,判断
绕点A旋转到如图2的位置,连接MN,判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)把等腰![]() 绕点A在平面内任意旋转,
绕点A在平面内任意旋转,![]() ,
,![]() ,请直接写出
,请直接写出![]() 的面积S的变化范围.
的面积S的变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解并解决问题:一般地,如果把一个图形绕着一个定点旋转一定角度![]() (
(![]() 小于
小于![]() )后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心.
)后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心.![]() 叫做这个旋转对称图形的一个旋转角.请依据上述定义解答下列问题:
叫做这个旋转对称图形的一个旋转角.请依据上述定义解答下列问题:
(1)请写出一个旋转对称图形,这个图形有一个旋转角是![]() .这个图形可以是______;
.这个图形可以是______;
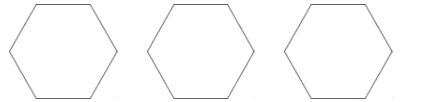
(2)为了美化环境,某中学需要在一块正六边形空地上分别种植六种不同的花草,现将这块空地按下列要求分成六块:①分割后的整个图形必须既是轴对称图形又是旋转对称图形;②六块图形的面积相同.请你按上述两个要求,分别在图中的三个正六边形中画出三种不同的分割方法(只要求画图正确,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,其中
两点,其中![]() ,
,![]() .该抛物线与
.该抛物线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() .
.

(1)求![]() 的值及该抛物线的解析式;
的值及该抛物线的解析式;
(2)如图2.若点![]() 为线段
为线段![]() 上的一动点(不与
上的一动点(不与![]() 重合).分别以
重合).分别以![]() 、
、![]() 为斜边,在直线
为斜边,在直线![]() 的同侧作等腰直角△
的同侧作等腰直角△![]() 和等腰直角△
和等腰直角△![]() ,连接
,连接![]() ,试确定△
,试确定△![]() 面积最大时
面积最大时![]() 点的坐标.
点的坐标.
(3)如图3.连接![]() 、
、![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() 为顶点的三角形与△
为顶点的三角形与△![]() 相似,若存在,请直接写出点
相似,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
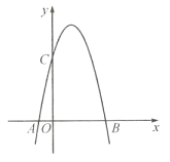
【题目】如图,一个二次函数的图像经过![]() 、
、![]() 、
、![]() 三点,点
三点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求这个二次函数的解析式;
(3)自变量![]() 在什么范围内时,
在什么范围内时,![]() 随
随![]() 的增大而增大?何时,
的增大而增大?何时,![]() 随
随![]() 的增大而减小
的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】罚球是篮球比赛中得分的一个组成部分,罚球命中率的高低对篮球比赛的结果影响很大.如图是对某球员罚球训练时命中情况的统计:
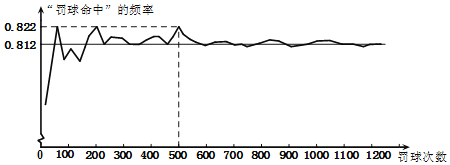
下面三个推断:①当罚球次数是500时,该球员命中次数是411,所以“罚球命中”的概率是0.822;②随着罚球次数的增加,“罚球命中”的频率总在0.812附近摆动,显示出一定的稳定性,可以估计该球员“罚球命中”的概率是0.812;③由于该球员“罚球命中”的频率的平均值是0.809,所以“罚球命中”的概率是0.809.其中合理的是( )
A.①B.②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
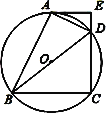
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD交CD的延长线于点E,DA平分∠BDE.
⑴求证:AE是⊙O的切线;
⑵若AE=4cm,CD=6cm,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )
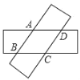
A.5 cmB.4.8 cmC.4.6 cmD.4 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com