
 如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O
如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O分析 (1)首先根据等腰三角形的性质得到∠ABC=∠ACB,然后利用高线的定义得到∠ECB=∠DBC,从而得证;
(2)首先求出∠A的度数,进而求出∠BOC的度数.
解答 (1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BD、CE是△ABC的两条高线,
∴∠BEC=∠BDC=90°
∴△BEC≌△CDB
∴∠DBC=∠ECB,BE=CD
在△BOE和△COD中
∵∠BOE=∠COD,BE=CD,∠BEC=∠BDE=90°
∴△BOE≌△COD,
∴OB=OC;
(2)∵∠ABC=50°,AB=AC,
∴∠A=180°-2×50°=80°,
∴∠DOE+∠A=180°
∴∠BOC=∠DOE=180°-80°=100°.
点评 本题考查了等腰三角形的性质及三角形的内角和定理;关键是掌握等腰三角形等角对等边.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
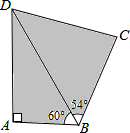 如图,四边形ABCD是一片水田,某村民小组需计算其面积,测得如下数据:
如图,四边形ABCD是一片水田,某村民小组需计算其面积,测得如下数据:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,C是线段BD上一点,分别以BC和CD为边长,在直线BD的同一侧作两个等边三角形,△ABC和△ECD,连接BE和AD,BE与AC交于点F,AD与CE交于点G.
如图,C是线段BD上一点,分别以BC和CD为边长,在直线BD的同一侧作两个等边三角形,△ABC和△ECD,连接BE和AD,BE与AC交于点F,AD与CE交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如果两个圆只有一个公共点,那么我们称这两个圆相切,这个公共点就叫做切点,当两圆相切时,如果其中一个圆(除切点外)在另一个圆的内部,叫做这两个圆内切;其中一个圆(除切点外)在另一个圆的外部,叫做这两个圆外切.如图所示:两圆的半径分别为R,r(R>r),两圆的圆心之间的距离为d,若两个圆外切则d=R+r,若两个圆内切则d=R-r,已知两圆的半径分别为方程x2+mx+3=0的两个根,当两圆相切时,已知这两个圆的圆心之间的距离为4,则m的值为-4或-2$\sqrt{7}$.
如果两个圆只有一个公共点,那么我们称这两个圆相切,这个公共点就叫做切点,当两圆相切时,如果其中一个圆(除切点外)在另一个圆的内部,叫做这两个圆内切;其中一个圆(除切点外)在另一个圆的外部,叫做这两个圆外切.如图所示:两圆的半径分别为R,r(R>r),两圆的圆心之间的距离为d,若两个圆外切则d=R+r,若两个圆内切则d=R-r,已知两圆的半径分别为方程x2+mx+3=0的两个根,当两圆相切时,已知这两个圆的圆心之间的距离为4,则m的值为-4或-2$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,⊙P经过点A(0,$\sqrt{3}$)、O(0,0)、B(1,0),点C在第一象限的$\widehat{AB}$上,则∠BCO的度数为30°.
如图,⊙P经过点A(0,$\sqrt{3}$)、O(0,0)、B(1,0),点C在第一象限的$\widehat{AB}$上,则∠BCO的度数为30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x+3y=300\\ 0<x<y<300\end{array}\right.$ | |
| B. | $\left\{\begin{array}{l}{x+3y=300}\\{0<x<y<300}\\{x、y是奇数}\end{array}\right.$ | |
| C. | $\left\{\begin{array}{l}{x+3y=300}\\{0<3x=y<300}\\{x、y是奇数}\end{array}\right.$ | |
| D. | $\left\{\begin{array}{l}{x+3y=300}\\{0<x<300,0<y<300}\\{x、y是奇数}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com