
【题目】如图,在正方形ABCD内一点E连接BE、CE,过C作CF⊥CE与BE延长线交于点F,连接DF、DE.CE=CF=1,DE=![]() ,下列结论中:①△CBE≌△CDF;②BF⊥DF;③点D到CF的距离为2;④S四边形DECF=
,下列结论中:①△CBE≌△CDF;②BF⊥DF;③点D到CF的距离为2;④S四边形DECF=![]() +1.其中正确结论的个数是( )
+1.其中正确结论的个数是( )
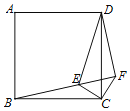
A.1B.2C.3D.4
【答案】B
【解析】
根据正方形的性质、全等三角形的判定和性质、勾股定理等知识逐项判断即可.
解:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°,
∵CF⊥CE,
∴∠ECF=∠BCD=90°,
∴∠BCE=∠DCF,
在△BCE与△DCF中,
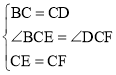 ,
,
∴△BCE≌△DCF(SAS),
故①正确;
∵△BCE≌△DCF,
∴∠CBE=∠CDF,
∴∠DFB=∠BCD=90°,
∴BF⊥ED,
故②正确,
过点D作DM⊥CF,交CF的延长线于点M,
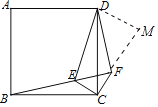
∵∠ECF=90°,FC=EC=1,
∴∠CFE=45°,
∵∠DFM+∠CFB=90°,
∴∠DFM=∠FDM=45°,
∴FM=DM,
∴由勾股定理可求得:EF=![]() ,
,
∵DE=![]() ,
,
∴由勾股定理可得:DF=2,
∵EF2+BE2=2BE2=BF2,
∴DM=FM=![]() ,故③错误,
,故③错误,
∵△BCE≌△DCF,
∴S△BCE=S△DCF,
∴S四边形DECF=S△DCF+S△DCE
=S△ECF+S△DEF
=S△AFP+S△PFB
=![]()
![]()
,故④错误,
故选:B.


科目:初中数学 来源: 题型:
【题目】某班学生在颁奖大会上得知该班获得奖励的情况如下表:
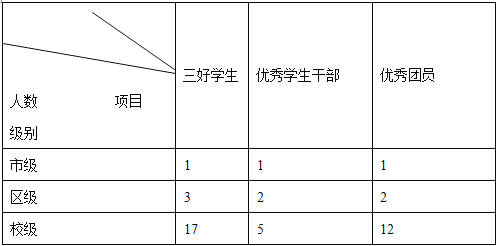
已知该班共有27人获得奖励(每位同学均可获得不同级别、不同类别多项奖励),其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的奖励为( )
A. 3项 B. 4项 C. 5项 D. 6项
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() ,线段
,线段![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始绕着点
开始绕着点![]() 以
以![]() 的速度顺时针旋转一周回到点
的速度顺时针旋转一周回到点![]() 后停止,点
后停止,点![]() 同时出发沿射线
同时出发沿射线![]() 自
自![]() 点向
点向![]() 点运动,若点
点运动,若点![]() 、
、![]() 两点能恰好相遇,则点
两点能恰好相遇,则点![]() 运动的速度为________
运动的速度为________![]() ;
;

![]() 将一副三角板中的两块直角三角尺的直角顶点
将一副三角板中的两块直角三角尺的直角顶点![]() 按如图方式叠放在一起(其中,
按如图方式叠放在一起(其中,![]() ,
,![]() ,
,![]() ;
;![]() ).将三角尺
).将三角尺![]() 固定,另一三角尺
固定,另一三角尺![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 转动,转动速度与
转动,转动速度与![]() 问中
问中![]() 点速度相同,当
点速度相同,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 有可能的值及对应转动的时间;若不存在,请说明理由.
有可能的值及对应转动的时间;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图像为直线
的图像为直线![]() .
.
(1)若直线![]() 与正比例函数
与正比例函数![]() 的图像平行,且过点(0,2),求直线
的图像平行,且过点(0,2),求直线![]() 的函数表达式;
的函数表达式;
(2)若直线![]() 过点(3,0),且与两坐标轴围成的三角形面积等于3,求
过点(3,0),且与两坐标轴围成的三角形面积等于3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为直径,
为直径,![]() 为弦.过
为弦.过![]() 延长线上一点
延长线上一点![]() ,作
,作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
(1)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图(2),∠BDC的平分线分别交AC,BC于点E,F,求∠CEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需280元;购买3个A品牌和1个B品牌的计算器共需210元.
(Ⅰ)求这两种品牌计算器的单价;
(Ⅱ)开学前,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的九折销售,B品牌计算器10个以上超出部分按原价的七折销售.设购买x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1,y2关于x的函数关系式.
(Ⅲ)某校准备集体购买同一品牌的计算器,若购买计算器的数量超过15个,购买哪种品牌的计算器更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1B2,△A2B2B3,△A3B3B4,…均为等边三角形.若OB1=1,则△A8B8B9的边长为( )
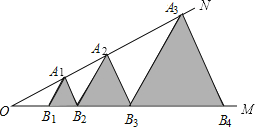
A.64B.128C.132D.256
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:△DEF是等边三角形.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com