
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,DA与⊙O相切于点A,DA=DC=![]() .
.

(1)求证:DC是⊙O的切线;
(2)若∠CAB=30°,求阴影部分的面积.
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,完成下列各题:
,完成下列各题:
(1)将函数关系式用配方法化为 y=a(x+h)2+k形式,并写出它的顶点坐标、对称轴.
(2)若它的图象与x轴交于A、B两点,顶点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级为了解课堂发言情况,随机抽取了该年级部分学生,对他们某天在课堂上发言次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知![]() 、
、![]() 两组发言人数的比为
两组发言人数的比为![]() ,请结合图表中相关信息,回答下列问题:
,请结合图表中相关信息,回答下列问题:
组别 | 发言次数 |
|
|
|
|
|
|
|
|
|
|
|
|

(1)求出样本容量,并补全条形统计图;
(2)求![]() 组所在扇形的圆心角的度数;
组所在扇形的圆心角的度数;
(3)该年级共有学生800人,请你估计该年级在这天里发言次数不少于12的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业开展献爱心扶贫活动,将购买的60吨大米运往贫困地区帮扶贫困居民,现有甲、乙两种货车可以租用.已知一辆甲种货车和3辆乙种货车一次可运送29吨大米,2辆甲种货车和3辆乙种货车一次可运送37吨大米.
(1)求每辆甲种货车和每辆乙种货车一次分别能装运多少吨大米?
(2)已知甲种货车每辆租金为500元,乙种货车每辆租金为450元,该企业共租用8辆货车.请求出租用货车的总费用w(元)与租用甲种货车的数量x(辆)之间的函数关系式.
(3)在(2)的条件下,请你为该企业设计如何租车费用最少?并求出最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为提升硬件设施,决定采购80台电脑,现有A,B两种型号的电脑可供选择.已知每台A型电脑比B型的贵2000元,2台A型电脑与3台B型电脑共需24000元.
(1)分别求A,B两种型号电脑的单价;
(2)若A,B两种型号电脑的采购总价不高于38万元,则A型电脑最多采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某相宜本草护肤品专柜计划在春节前夕促销甲、乙两款护肤品,根据市场调研,发现如下两种信息:
信息一:销售甲款护肤品所获利润y(元)与销售量x(件)之间存在二次函数关系y=ax2+bx.在x=10时,y=140;当x=30时,y=360.
信息二:销售乙款护肤品所获利润y(元)与销售量x(件)之间存在正比例函数关系y=3x.请根据以上信息,解答下列问题;
(1)求信息一中二次函数的表达式;
(2)该相宜本草护肤品专柜计划在春节前夕促销甲、乙两款护肤品共100件,请设计一个营销方案,使销售甲、乙两款护肤品获得的利润之和最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△BCD中,DF⊥BC于点F,点A为直线DF上一动点,以B为旋转中心,把BA顺时针方向旋转60°至BE,连接EC.
(1)当点A在线段DF的延长线上时,
①求证:DA=CE;
②判断∠DEC和∠EDC的数量关系,并说明理由;
(2)当∠DEC=45°时,连接AC,求∠BAC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
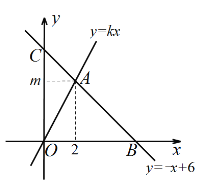
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 的图象与正比例函数
的图象与正比例函数![]() 的图象交于点A(2,m),一次函数
的图象交于点A(2,m),一次函数![]() 的图象分别与x轴、y轴交于B、C两点.
的图象分别与x轴、y轴交于B、C两点.
(1)求m、k的值;
(2)求∠ACO的度数和线段AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com