
| r |
| h |
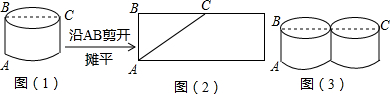
 (2)如图(2).
(2)如图(2).| r |
| h |
| 4 |
| π2-4 |
| 10 |
| π2-4 |
| 10 |
| π2-4 |
| 10 |
| π2-4 |


科目:初中数学 来源: 题型:
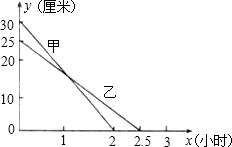 在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间X(小时)之间的关系如图所示.
在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间X(小时)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
 某校初三年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球,共投10次,甲、乙两名同学测试情况如图所示.
某校初三年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球,共投10次,甲、乙两名同学测试情况如图所示.| 平均数 | 众数 | 方差 | |
| 甲 | |||
| 乙 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
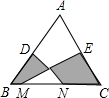 如图,在△ABC中,AB=AC,D、E分别是AB、AC的中点,M、N为BC上的点,连接DN、EM.若AB=10cm,BC=12cm,MN=6cm,则图中阴影部分的面积为
如图,在△ABC中,AB=AC,D、E分别是AB、AC的中点,M、N为BC上的点,连接DN、EM.若AB=10cm,BC=12cm,MN=6cm,则图中阴影部分的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,PA、PB切⊙O于A、B,D是弧AB上任一点,过点D作⊙O的切线交PA、PB于点E、F.
如图,PA、PB切⊙O于A、B,D是弧AB上任一点,过点D作⊙O的切线交PA、PB于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:
 现有一个顶角为36°的等腰三角形,将其分割成4个等腰三角形(根据要求画出图形,标出底角度数),4个等腰三角形满足如下各自条件:
现有一个顶角为36°的等腰三角形,将其分割成4个等腰三角形(根据要求画出图形,标出底角度数),4个等腰三角形满足如下各自条件:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com