
如图,直线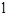 与⊙O相切于点D,过圆心O作EF∥
与⊙O相切于点D,过圆心O作EF∥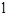 交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线
交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线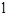 于B、C两点;
于B、C两点;

(1)求证:∠ABC+∠ACB=90°;
(2)若⊙O的半径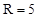 ,BD=12,求tan∠ACB的值.
,BD=12,求tan∠ACB的值.
解(1)证明:如图,∵EF是⊙O的直径,∴∠EAF=90°。∴∠ABC+∠ACB=90°。
(2)连接OD,则OD⊥BD,过点E作EH⊥BC,垂足为点H,

∴ EH∥OD。
∵EF∥BC,EH∥OD, OE=OD,
∴四边形EODH是正方形 。∴EH=HD=OD=5。
∵BD=12,∴BH=7。
在Rt△BEH中,tan∠BEH= 。
。
又∵∠ABC+∠BEH=90°,∠ABC+∠ACB=90°,
∴∠ACB=∠BEH。∴tan∠ACB 。
。
【解析】(1)由直径所对圆周角是直角的性质和三角形内角和定理可得结论。
(2)求出tan∠BEH= ,由∠ACB=∠BEH可得结论。
,由∠ACB=∠BEH可得结论。


科目:初中数学 来源: 题型:
 如图,PA与⊙O相切于点A,弦AB⊥OP,垂足为C,OP与⊙O相交于点D,已知OA=2,OP=4.
如图,PA与⊙O相切于点A,弦AB⊥OP,垂足为C,OP与⊙O相交于点D,已知OA=2,OP=4.查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省广州白云区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,直线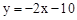 与
与 轴交于点A,直线
轴交于点A,直线 交于点B,点C在线段AB上,⊙C与
交于点B,点C在线段AB上,⊙C与 轴相切于点P,与OB切于点Q.
轴相切于点P,与OB切于点Q.
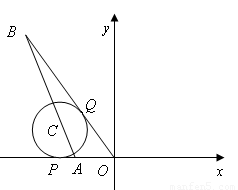
求:(1)A点的坐标;
(2)OB的长;
(3)C点的坐标.
查看答案和解析>>
科目:初中数学 来源:2010年天津市河北区中考数学一模试卷(解析版) 题型:选择题
 与x轴、y 轴分别交于A、B两点,已知点C(0,-1)、D(0,k),且0<k<3,以点D为圆心、DC为半径作⊙D,当⊙D与直线AB相切时,k的值为( )
与x轴、y 轴分别交于A、B两点,已知点C(0,-1)、D(0,k),且0<k<3,以点D为圆心、DC为半径作⊙D,当⊙D与直线AB相切时,k的值为( )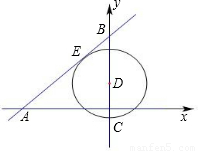




查看答案和解析>>
科目:初中数学 来源:2011年四川省中考模拟试题数学卷 题型:选择题
1.
如图,直线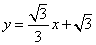 与
与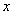 轴、
轴、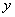 轴分别相交于
轴分别相交于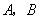 两点,圆心
两点,圆心 的坐标为
的坐标为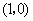 ,圆
,圆 与
与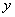 轴相切于点
轴相切于点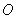 .若将圆
.若将圆 沿
沿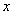 轴向左移动,当圆
轴向左移动,当圆 与该直线相交时,横坐标为整数的点
与该直线相交时,横坐标为整数的点 的个数是( )
的个数是( )
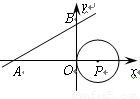
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com