
如图所示,已知△ABC中,AD⊥BC于D,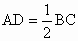 ,E、F分别是AB、AC的中点,以EF为直径作半圆O.
,E、F分别是AB、AC的中点,以EF为直径作半圆O.
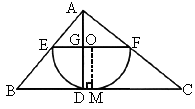
求证:BC是半圆O的切线.
|
证明:连接 EF,交AD于G,过圆心O作OM⊥BC,垂足为 M.∵ E、F分别是AB、AC的中点,∵ 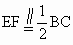 , ,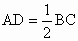 . .
∴ EF=AD,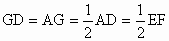 , ,
∴ 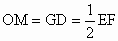 . .
∴ OM为半圆O的半径.又 OM⊥BC,∴ BC是半圆O的切线.证明圆的切线有以下两种方法:方法一是依据切线的定义,圆心到直线的距离等于半径,则该直线是圆的切线,方法二是依据判定定理,过半径外端点并且垂直于半径的直线是圆的切线.选择哪种方法关键是在已知条件中寻找.若不能判定直线 l与⊙O有公共点,则使用方法一,过圆心O作l的垂线OP,证明OP等于半径,方法二简述为“作垂直,证半径”;若能判定直线l与⊙O有公共点A,则使用方法二,连接圆心O与点A,证明半径OA⊥l,方法二简述为“连半径,证垂直”. |
|
本题考查直线与圆的位置关系,题中线段BC与⊙O的公共点没有确定,故需添加辅助线.过点O作OM⊥BC,证明 |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com