
分析 根据题意画出图形,利用当圆A与以CD为半径的圆C相外切以及当圆A与以CD为半径的圆C相内切,分别求出半径,即可确定半径R的取值范围.
解答 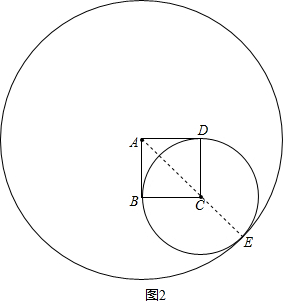
 解:∵正方形ABCD的边长为1,
解:∵正方形ABCD的边长为1,
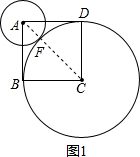
∴如图1,当圆A与以CD为半径的圆C相外切,
∵AC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,BC=CD=FC=1,
AF+FC=AC,
∴AF=AC-FC=$\sqrt{2}$-1,
如图2,当圆A与以CD为半径的圆C相内切,
∵AC═$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,BC=CD=EC=1,
AC+EC=AE,
∴AE=AC+EC=$\sqrt{2}$+1,
综上所述:圆A的半径R的取值范围为:$\sqrt{2}$-1<R<$\sqrt{2}$+1,
故答案为:$\sqrt{2}$-1<R<$\sqrt{2}$+1.
点评 此题主要考查了相切两圆的性质以及正方形的性质,根据已知进行分类讨论得出是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校为了解全校1600名学生每周课外体育活动时间的情况,随机调查了其中的部分学生,对这些学生每周课外体育活动时间x(单位:小时)进行了统计,根据所得数据绘制了一幅统计图,根据以上信息及统计图解答下列问题
某校为了解全校1600名学生每周课外体育活动时间的情况,随机调查了其中的部分学生,对这些学生每周课外体育活动时间x(单位:小时)进行了统计,根据所得数据绘制了一幅统计图,根据以上信息及统计图解答下列问题查看答案和解析>>
科目:初中数学 来源: 题型:填空题
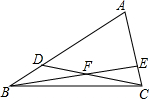 在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为72.
在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为72.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{m-a}{b}$分钟 | B. | $\frac{m}{a+b}$分钟 | C. | $\frac{m-a+b}{b}$分钟 | D. | $\frac{m-a-b}{b}$分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (5,1) | B. | (-1,5) | C. | (-3,-$\frac{5}{3}$) | D. | ($\frac{5}{3}$,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com