
 如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB项点B移动,设P、Q两点移动t秒(0<t<5)后,三角形CPQ的面积为S米2.
如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB项点B移动,设P、Q两点移动t秒(0<t<5)后,三角形CPQ的面积为S米2.分析 (1)过点P作PE⊥BC于E,利用勾股定理求出AC的长,AP=2t,CQ=t,则PC=10-2t,又PE∥AB,根据平行线分线段成比例列出比例式即可得出PE的长,再由三角形的面积公式即可得出结论;
(2)假设四边形ABQP与△CPQ的面积相等,则S△PCQ=$\frac{1}{2}$S△ABC,再判断出方程根的情况即可;
(3)分∠PQC=90°与∠CPQ=90°两种情况进行讨论即可.
解答 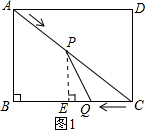 解:(1)如图1,过点P作PE⊥BC于E,Rt△ABC中,AC=$\sqrt{{AB}^{2}+{BC}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10(m).
解:(1)如图1,过点P作PE⊥BC于E,Rt△ABC中,AC=$\sqrt{{AB}^{2}+{BC}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10(m).
由题意知:AP=2t,CQ=t,则PC=10-2t.
由AB⊥BC,PE⊥BC,得PE∥AB,
∴$\frac{PE}{AB}$=$\frac{PC}{AC}$,即$\frac{PE}{6}$=$\frac{10-2t}{10}$
∴PE=$\frac{3}{5}$(10-2t)=-$\frac{6}{5}$t+6,
∴S△PCQ=$\frac{1}{2}$CQ•PE=$\frac{1}{2}$t•(-$\frac{6}{5}$t+6)=-$\frac{3}{5}$t2+3t(0<t<5);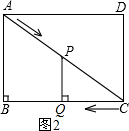
(2)不能.
理由:∵假设四边形ABQP与△CPQ的面积相等,
∴S△PCQ=$\frac{1}{2}$S△ABC,即-$\frac{3}{5}$t2+3t=$\frac{1}{2}$×6×8,整理得,t2-5t+40=0.
∵△=(-5)2-160=-135<0,
∴t无解,
∴边形ABQP与△CPQ的面积不能相等;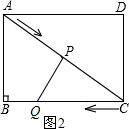
(3)如图2,当∠PQC=90°时,PQ⊥BC,
∵AB⊥BC,AB=6,BC=8,QC=t,PC=10-2t,
∴△PQC∽△ABC,
∴$\frac{PC}{AC}$=$\frac{CQ}{BC}$,即$\frac{10-2t}{10}$=$\frac{t}{8}$,解得t=$\frac{40}{13}$(秒);
如图3,当∠CPQ=90°时,PQ⊥AC,
∵∠ACB=∠QCP,∠B=∠QPC,
∴△CPQ∽△CBA,
∴$\frac{CP}{BC}$=$\frac{CQ}{AC}$,即$\frac{10-2t}{8}$=$\frac{t}{10}$,解得t=$\frac{25}{7}$(秒).
综上所述,t为$\frac{40}{13}$秒与$\frac{25}{7}$秒时,△CPQ为直角三角形.
点评 本题考查的是四边形综合题,涉及到矩形的性质、勾股定理、根的判别式、三角形的面积公式及平行线分线段成比例等知识,解题关键是对这些知识的熟练掌握及灵活运用,在解答(3)时要注意分类讨论.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源:2016-2017学年吉林省七年级下学期期中数学模拟试卷(四)(解析版) 题型:单选题
下列四个算式:①(﹣a)3•(﹣a2)2=﹣a7;②(﹣a3)2=﹣a6;③(﹣a3)3÷a4=﹣a2;④(﹣a)6÷(﹣a)3=﹣a3中,正确的有( )
A. 0个 ; B. 1个; C. 2个; D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
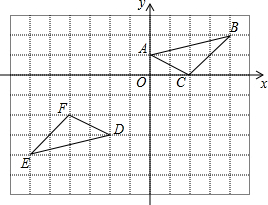 如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(4,2),C的坐标为(2,0),将△ABC绕点P旋转180°得到△DEF,则旋转中心点P的坐标为( )
如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(4,2),C的坐标为(2,0),将△ABC绕点P旋转180°得到△DEF,则旋转中心点P的坐标为( )| A. | (-1,-1) | B. | (-1,-2) | C. | (-2,-1) | D. | (-2,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
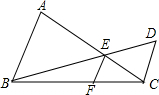 如图,AB∥CD,AC、BD交于点E,EF∥CD交BC于F.求证:
如图,AB∥CD,AC、BD交于点E,EF∥CD交BC于F.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是某校美术室的一个道具,它是由棱长均为10dm的小立方块搭成的,工人师傅要将其表面(底面除外)涂上油漆,请你计算一下,工人师傅至少需涂多少平方米的油漆?
如图,是某校美术室的一个道具,它是由棱长均为10dm的小立方块搭成的,工人师傅要将其表面(底面除外)涂上油漆,请你计算一下,工人师傅至少需涂多少平方米的油漆?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com