
【题目】每年农历五月初五,是中国民间的传统节日——端午节.它始于我国的春秋战国时期,已列为世界非物质文化遗产.时至今日,端午节在我国仍是一个十分盛行的节日.今年端午节,某地甲、乙两家超市为吸引更多的顾客,开展促销活动,对某种质量和售价相同的粽子分别推出了不同的优惠方案.甲超市的方案是:购买该种粽子超过80元后,超出80元的部分按九折收费;乙超市的方案是:购买该种粽子超过120元后,超出120元的部分按八折收费.请根据顾客购买粽子的金额,选择到哪家超市购买粽子划算?
【答案】当顾客购买粽子的金额不超过80元或等于160元时,顾客到甲、乙超市购买粽子花费都一样;当顾客购买粽子的金额超过80元且小于160元时,顾客到甲超市购买粽子划算;当顾客购买粽子的金额超过160元时,顾客到乙超市购买粽子划算.
【解析】
设累计购物x元,分x≤80、80<x≤120和x>120三种情况进行讨论,当x>120时,再分到甲优惠、到乙优惠和到两超市花费一样分别列出不等式和方程求解即可.
解:设顾客购买粽子的金额为![]() 元.
元.
(1)当![]() 时,在甲、乙两超市购买粽子都不享受优惠,且两超市以同样的质量和价格出售同样的商品,因此顾客到甲、乙超市购买粽子花费都一样.
时,在甲、乙两超市购买粽子都不享受优惠,且两超市以同样的质量和价格出售同样的商品,因此顾客到甲、乙超市购买粽子花费都一样.
(2)当![]() 时,甲超市购买粽子优惠,乙超市购买粽子不优惠,因此顾客到甲超市购买粽子划算.
时,甲超市购买粽子优惠,乙超市购买粽子不优惠,因此顾客到甲超市购买粽子划算.
(3)当![]() 时,
时,
①若顾客到甲超市购买粽子划算,则![]() .解得
.解得![]() .因此当
.因此当![]() 时,顾客到甲超市购买粽子划算.
时,顾客到甲超市购买粽子划算.
②若顾客到乙超市购买粽子划算,则![]() .解得
.解得![]() .因此当
.因此当![]() 时,顾客到乙超市购买粽子划算.
时,顾客到乙超市购买粽子划算.
③若![]() ,解得
,解得![]() .
.
因此当![]() 时,顾客到甲、乙两家超市购买粽子花费都一样.
时,顾客到甲、乙两家超市购买粽子花费都一样.
答:当顾客购买粽子的金额不超过80元或等于160元时,顾客到甲、乙超市购买粽子花费都一样;当顾客购买粽子的金额超过80元且小于160元时,顾客到甲超市购买粽子划算;当顾客购买粽子的金额超过160元时,顾客到乙超市购买粽子划算.


科目:初中数学 来源: 题型:
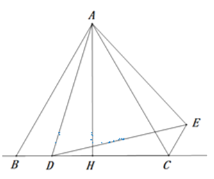
【题目】如图,在![]() 中,
中,![]() ,
,![]() 垂足为
垂足为![]() ,
,![]() 为直线
为直线![]() 上一动点(不与点
上一动点(不与点![]() 重合),在
重合),在![]() 的右侧作
的右侧作![]() ,使得
,使得![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)当![]() 在线段
在线段![]() 上时
上时
① 求证:![]() ≌
≌![]() ;
;
② 若![]() , 则
, 则![]() ;
;
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
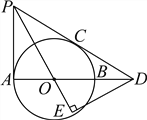
【题目】如图,AB是⊙O的直径,PA、PC与⊙O分别相切于点A、C,PC交AB的延长线于点D.DE⊥PO交PO的延长线于点E.
(1)求证:∠EPD=∠EDO;
(2)若PC=6,tan∠PDA=![]() ,求OE的长.
,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
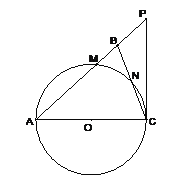
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求⊙O的半径及△ACP的周长.
,求⊙O的半径及△ACP的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
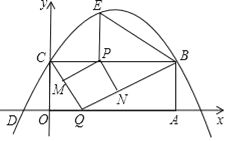
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE和Rt△OCD中的一个角相等?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠AGE,∠D=∠DGC
(1)求证:AB∥CD;
(2)若∠1+∠2=180°,求证:∠BEC+∠B=180°;
(3)在(2)的基础上,若∠BEC=2∠B+30°,求∠C的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
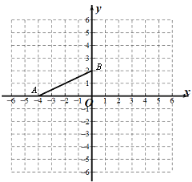
【题目】如图,在平面直角坐标系中,已知点A(-4,0)、B(0,2),点P(a,a).
(1)当a=2时,将△AOB绕点P(a,a)逆时针旋转90°得△DEF,点A的对应点为D,点O的对应点为E,点B的对应点为点F,在平面直角坐标系中画出△DEF,并写出点D的坐标 ;
(2)作线段AB关于P点的中心对称图形(点A、B的对应点分别是G、H),若四边形ABGH是正方形,则a= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是AD和BC上的两点,EF将四边形ABCD分成两个边长为5cm的正方形,∠DEF=∠EFB=∠B=∠D=90°;点H是CD上一点且CH=lcm,点P从点H出发,沿HD以lcm/s的速度运动,同时点Q从点A出发,沿A→B→C以5cm/s的速度运动.任意一点先到达终点即停止运动;连结EP、EQ.

(1)如图1,点Q在AB上运动,连结QF,当t= 时,QF//EP;
(2)如图2,若QE⊥EP,求出t的值;
(3)试探究:当t为何值时,![]() 的面积等于
的面积等于![]() 面积的
面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
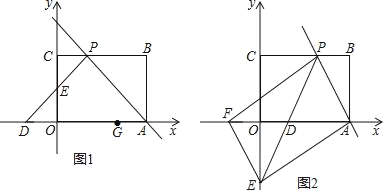
【题目】如图1,矩形OABC摆放在平面直角坐标系中,点A在x轴上,点C在y轴上,OA=3,OC=2,过点A的直线交矩形OABC的边BC于点P,且点P不与点B、C重合,过点P作∠CPD=∠APB,PD交x轴于点D,交y轴于点E.
(1)若△APD为等腰直角三角形.
①求直线AP的函数解析式;
②在x轴上另有一点G的坐标为(2,0),请在直线AP和y轴上分别找一点M、N,使△GMN的周长最小,并求出此时点N的坐标和△GMN周长的最小值.
(2)如图2,过点E作EF∥AP交x轴于点F,若以A、P、E、F为顶点的四边形是平行四边形,求直线PE的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com